第一章 引言
价值溢价异象是指价值股(低市值账面比)的收益超过成长股(高市值账面比)收益的现象,已在全球许多股票市场中得到了验证。FamaandFrench(1992)利用组合排序法对美国股市 1963 年至 1990 年的数据进行价值效应研究,在每年底按照账面市值比排序,将股票分为十个组合,然后比较价值股组合和成长股组合在随后一年的收益率,发现价值股可获取高于成长股 18.36%的年度收益。与此对应,Lakonishok 等 (1994)用美国股市 1968 年至 1989 年进行了类似的实证研究。不过,他们没有采用每年重新构造组合的方法,而是采用买入并持有策略,以考察价值投资的长期表现。实证结果显示,在 5 年的检验期内,价值股和成长股的平均年度收益分别为 19.8%和 9.3%,可以看出平均而言价值股的回报好于成长股,价值溢价为 10.5%。而经规模因素调整后,价值溢价下降为 7.8%。后来,Fama and French (2012)以及 Cakici (2013)的实证结果显示,1990 年至 2012年的美国股市同样存在价值溢价现象。FamaandFrench(1998)将研究范围扩展到13 个国家,发现有 12 个国家的股票市场都存在价值溢价现象。这说明,价值溢价不是美股市场的特有现象,其存在具有普遍性。Asness,MoskowitzandPedersen(2013))在 8 个不同的市场和资产类别分别检验价值溢价效应和动量效应,发现价值溢价效应与动量效应是普遍存在的,二者之前存在负相关关系。而 Golubovand Konstantinidi (2019) 首次将 Rhodes-Kropf, Robinson, and Viswanathan (2004)在研究并购浪潮时使用的分解法(以下简称为 RRV 分解)引入价值溢价的研究中,将市值账面比分解为市值价值比和价值账面比后,发现只有市值价值比是带来价值溢价的原因。受这一研究方法的启发,我们尝试将 RRV 分解法引入 A 股市场中价值溢价效应的检验。
........................
第二章 市值账面比及其成分的收益率预测性检验
第一节 组合排序
一、单变量组合排序
我们对市值账面比及其组成部分先使用组合排序的方法进行研究,在每年的6 月 30 日,将股票按照市值账面比或其组成部分共五个指标进行分组,以形成投资组合。沿用 Asparouhova, Bessembinder, and Kalcheva (2013)的做法,我们使用上一期毛收益率加权法(RW)和市值加权法(VW)分别计算投资组合总收益率,这两种加权方法都能够避免在等权重投资组合中由于微观结构噪声引起的收益率测量误差。此外,由于在市值加权法中,小股票的权重较小,而小市值股票的价值溢价一般较大,价值溢价在一定程度上会被低估,因此我们使用两种投资组合加权方法。同时我们也会做以规模(即市值)为条件的双变量排序。
表 3.1 的 A 部分展示了在投资组合形成后的 12 个月内,按市值账面比或其组成部分排序的 10 个 RW 投资组合的平均月收益率。结果显示,按市值账面比排序分组时,收益率随着市值账面比的增大呈递减趋势,差分组合平均每月产生0.55%的回报,但在统计上不太显著,年化夏普比率为 0.23。按总误差排序分组时,随着总误差增大,收益率的递减趋势更加明显,差分组合每月产生 1.12%的收益,但波动性较低,因此夏普比率拉高到 0.75。按公司特定估值误差排序分组时,差分组合的收益率进一步增加为每月 1.32%,但由于波动性进一步降低,夏普比率拉高至 0.89。最后,按行业估值误差和价值账面比排序的差分组合每月分别产生约 0.18%和-0.48%的收益,并且在统计上不显著,夏普比率均小于 0。
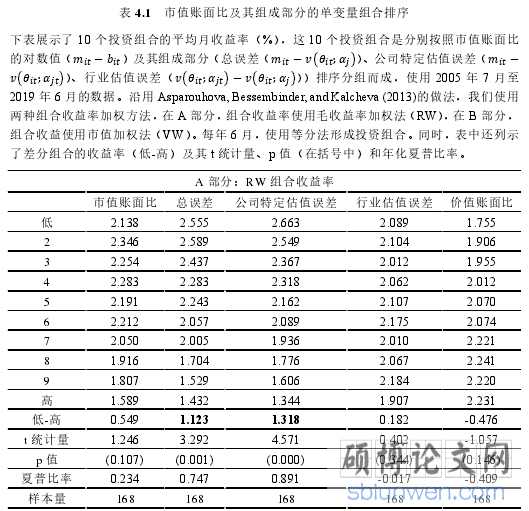
表 4.1 市值账面比及其组成部分的单变量组合排序
第二节 公司层面的收益率回归
一、 WLS 回归
本节我们用个股月收益率对市值账面比、其组成部分以及其他已知的可预测股票收益的公司特征分月份进行 Fama-MacBeth 回归。
典型的 Fama-MacBeth 回归中采用 OLS 方法,意味着在各时期内各股票的权重相等。Asparouhova, Bessembinder, and Kalcheva (2010) 指出,在存在微观结构噪声的情况下,这种回归中的斜率系数可能会有偏,并建议使用上一期的毛收益率作为权重(RW 法),进行 WLS 回归,我们沿用这一方法,并在表3.3 中展示回归分析的结果。
在第 1 列,我们使用传统的市值账面比作为自变量,对未来的股票收益进行回归,得到市值账面比的系数显著为负,这与文献中的结论一致。在第 2列,我们使用两步分解中获得的总误差和价值账面比替换市值账面比进行回归。与组合排序的结果一致,我们发现总误差的系数显著为负,并且小于前一回归中市值账面比的系数,而价值账面比的系数在统计上不显著,说明剔除了价值账面比的扰动之后,总误差对于股票收益率的预测力增强了。在第 3 列,我们进一步将总误差分解为公司特定估值误差和行业估值误差,回归结果显示,公司特定估值误差与未来的股票收益率具有较强的负相关关系,而行业估值误差和价值账面比的回归系数均不显著,其中行业估值误差的系数为负,而
.............................
第三章 样本和数据 .........................6
第四章 市值账面比及其成分的收益率预测性检验 .............9
第一节 组合排序...........................9
一、单变量组合排序 ................................. 9
二、双变量组合排序 ............................. 12
第五章 卖空限制是价值溢价的成因吗?....................22
第一节 所有 A 股的组合排序检验......................22
第二节 融券标的的组合排序检验.........................26
第五章 卖空限制是价值溢价的成因吗?
第一节 所有 A 股的组合排序检验
过往学者的研究表明,受到卖空限制越大的股票产生的价值溢价更高,因为卖空限制使得股票价格持续的偏离其内在价值 ,GolubovandKonstantinidi(2019)使用市值账面比分解法在美股市场检验了这一理论,结果表明卖空限制与市值价值比部分相关,能够带来价值溢价。本章我们使用 A 股市场的样本来做同样的检验。
Nagel (2005) 认为,机构持股能够通过增加可出借证券数量的方式来促进卖空,并且证明了市值账面比效应在机构持股比例较低的公司更加明显。因此,我们使用机构持股比例作为卖空限制的代理变量,样本数据来自 Wind 数据库。我们使用市值账面比(或其组成部分)与剩余机构持股水平(RI)进行独立的双变量排序分组,得到 25 个投资组合,表 4.1 展示了使用 RW 加权方法构建投资组合的结果。
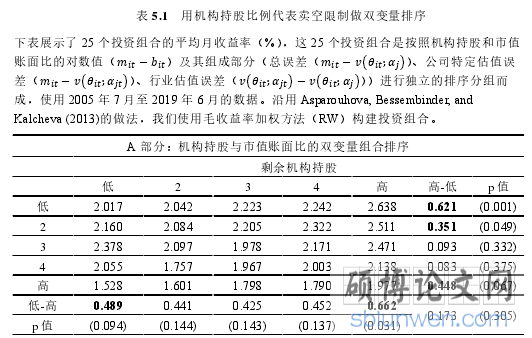
表 5.1 用机构持股比例代表卖空限制做双变量排序
.............................
第六章 结论
本文沿用 Golubov and Konstantinidi (2019) 采用的 RRV 分解法,首先将市值账面比分解为市值价值比和价值账面比,又进一步将市值价值比分解为公司特定估值误差和行业估值误差,以判断其中真正带来价值溢价的部分。研究发现,在单变量组合排序和双变量组合排序中,市值价值比,尤其是其中的公司特定估值误差部分,是市值账面比中带来价值溢价的主要部分,市值价值比(或公司特定估值误差)越低,股票未来获得的收益率越大。而行业估值误差和价值账面比则与价值溢价的形成无关,对应的差分组合策略并没有获得显著的收益。这一结论与 Golubov and Konstantinidi (2019)相同。
在进行横截面回归时,我们发现,当在模型中不加入控制变量时,回归结果与组合排序的结果一致,在市值账面比的各组成部分中,只有公司特定估值误差部分带来了收益。但是,在模型中加入代表公司特征的控制变量后,情况发生了变化。公司特定估值误差部分仍然能够显著的预测股票收益,同时,行业估值误差和价值账面比也与股票收益产生了显著的负相关。
因此,综合来看,市值价值比(或者其中的公司特定估值误差部分)被证明确实是带来价值溢价的原因,但关于行业估值误差和价值账面比的证据则不太充分。
此外,在市值账面比分解的基础上,我们对于价值溢价的卖空限制理论进行了检验。研究表明,在不允许卖空的股票组中存在显著的由市值价值比(公司特定估值误差)驱动的价值溢价效应,而在允许卖空的股票组中,不存在明显的价值溢价现象,说明在 A 股市场中,卖空限制确实是带来价值溢价的原因。而关于卖空限制程度的高低对价值溢价的影响大小,我们观察到,机构持股较低,也就是卖空限制程度较大的股票价值溢价相对更明显,但是这一结论没有得到充分的证据支撑。
参考文献(略)
