本文是一篇金融论文,本文仅仅在破产概率最小化以及期望终端盈余效用最大化下考虑再保险合约双方之间的比例再保险策略选择博弈,而对于优化目标的选择,还涉及破产分红红利最大化等目标。同时除比例再保险外,保险市场还存在停止损失再保险等,这些问题都还需要进一步探讨。
第一章 绪论
第一节 研究背景和意义
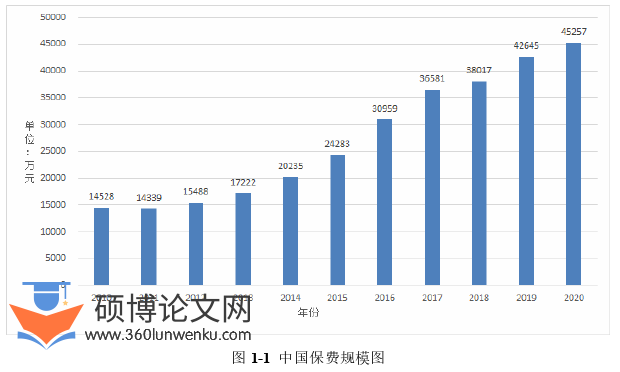
社会生存和发展的过程总是伴随着各种自然灾害和事故,如千万年前地球霸主恐龙的灭绝,庞贝古城的毁灭,震惊世界的911事件等。因此,人类为了规避风险,应对突发灾难与重大事故,产生了最原始的保险思想以减小对未来的不确定性。中国的保险思想最早可追溯到战国时期,商人为分散风险降低损失,于是选择将货物分装。我国保险思想源远流长,放眼如今,我国的保险市场规模与日俱增,各类保险公司已突破百家,财险公司、寿险公司和再保公司等保险公司的出现,也不断丰富着我国的保险市场。中国人口基数巨大,保费规模在2020年已突破45000亿元。图1-1展示了2010-2020年我国保费收取情况。
金融论文怎么写
尽管资金规模巨大,但保险公司“暴雷”事件近几年也不断出现在人们的视野中。在全世界范围内,保费“入不敷出”的情况在保险市场较为完善的发达国家也是常态。由保险精算原理可知,以财产保险为例,在时间跨度较大的情况下,尽管资金的流入与流出存在时间差,但保险公司的保费收入与赔付基本持平。需要注意的是当保险市场处于业务发展上升期时,由时间差所造成的资金净值变化是巨大的。造成此结果的原因有以下两点:超出保险公司预期的巨额赔款(如特大自然灾害)与时间价值的波动。
..............................
第二节 论文结构及内容
本文的主要工作和内容可分为以下五个部分;
第一章,绪论。本章内容主要为对研究背景的概述,介绍研究目的与意义,展示研究内容与结构,以及本文的创新点与不足。
第二章,文献综述。本章主要梳理与总结研究过程中涉及的文献。为了使相关文献更加条理清晰,并突出本文研究的意义,主要从破产概率目标下保险公司的最优再保险策略选择、期望效用最大化下保险公司的最优再保险策略选择,以及保险公司与再保险公司间的再保险策略选择博弈三个方面介绍了国内外的研究现状。
第三章,破产概率目标下再保险策略选择博弈。假设保险公司以破产概率减小作为购买比例再保险的条件,同时再保险公司也以相同目标作为承保的依据。在扩散风险模型下,利用鞅方法和最优化理论得到了不同博弈情形下最优比例再保险策略以及再保费的取值范围。
第四章,期望终端盈余效用最大化下再保险策略选择博弈。假设再保险合约成立条件为再保险合约双方期望终端盈余效用的增加。同样在扩散风险模型下,假设再保险合约双方均具有投资行为,考虑了比例再保险策略选择博弈问题。假设两公司都具有指数效用函数,通过构造并求解HJB方程,得到了不同博弈情形下最优投资-再保险策略,以及再保费的取值范围。
第五章,总结与展望。总结本文的研究内容,并讨论论文可能存在的不足之处,以及可以进一步研究的问题。
............................
第二章 文献综述
第一节 破产概率约束下最优再保险策略选择
作为保险领域非常经典的研究方法,学者们对破产概率的研究至今已有超过一百年的历史。1909年第六届国际精算师大会上Alf Goldberg首次提出了以破产概率研究再保险的理论,即便是理论研究日趋完善的今天,仍有不少学者使用破产概率最小化方法进行再保险研究。保险公司作为金融机构,为投保人提供保障,降低投保人风险是其主要业务,因此降低破产概率是保险公司追求的目标之一。以自留风险最小化为目标,Dickson(1997)研究了再保险策略选择问题。在此基础之上Højgaard与Taksar(1998)选择扩散模型拟合保险公司财富过程,且将交易成本加入到模型之中。当优化目标为保险公司调节系数且满足纯费率原则时,Bulmann(1980),Deprez和Gerber(1985)也进行了相关再保险问题的研究。El Abderrahim (2020)讨论了一种随机最优控制问题,以确定最优风险管理策略,其目的是为比例再保险合同确定最合适的转移率水平。考虑经典的Cramer-Lundberg风险模型,当保险公司选择比例再保险,且以破产概率的减小作为优化目标时,Schmidli(2001)计算得出最优再保险策略的常数表达式,并给出了最小破产概率的具体形式。也有学者选择复合Poisson过程用于拟合保险公司的盈余情况,以破产概率为约束,Hipp和Vogt(2003)得到了最优无限制超额损失再保险策略。
同样选择 Cramer-Lundberg模型,当保险公司可以投资在险资产时,Hipp和Plum(2000)以破产概率最小化为目标研究再保险策略。但需要注意的是,在Hipp和Plum(2000)的模型中,隐含债券的利率为零。为了得到进一步的结果,在此基础上,Liu和Yang(2004)考虑了非零的利率,研究了相同的问题,然而在利率不为零时无法求得闭形式的解。在过去的研究中,学者们大多采用最优化理论研究再保险策略选择问题。使用同样的方法,Browne(1995),Schmidli(2001)将研究进一步深化,先后研究了再保险购买比例与风险资产的投资量对再保险合约的影响,在保险索赔过程为带漂移的布朗运动前提下,求得了保险公司的最小破产概率表达式。考虑保险公司生存概率问题,罗琰、杨招军和杨金强(2009)分别以最长经营时间与最大生存概率为目标,得到了再保险与投资的最优策略。对于延迟索赔风险模型,肖鸿民,王占魁和刘月娣(2020)在方差分保费原则计算原理下也进行了相关研究。Han等(2020)以最小化包含绝对破产概率和模型模糊性惩罚的鲁棒值为目标,求得最优再保险策略与值函数表达式。Kasumo等(2018)发现,对于Cramér-Lundberg模型和扩散扰动模型,比例再保险增加了公司在轻尾和重尾分布下的生存概率
..............................
第二节 期望效用最大化最优再保险策略选择
最大化终端效用是学者们研究保险公司利益最常使用的目标,而其理论基础——期望效用理论于1944年由Neuman和Morgenstem首次提出。在零效用保费计算原则下,Wang和Dhaene(1998)证明了保费分配满足帕累托最优分配原则。以期望净收益最大为目标,Gajek等(2000)也做了相关研究。周明等(2010,2013)考虑了保险公司风险调整资本收益率与夏普比率,并以此为优化目标,求得了保险公司最优分保策略表达式。除此以外,当保险公司选择停止损失再保险时,追求期望折现分红总量最大化,Choulli等(2001),Golubin (2016)分别研究了公司负债,最大期望效用的最优再保险问题。当限制投资人不允许卖空股票时,为追求保险公司期望终端盈余效用最大化,Bai和Guo(2010),张强和陈萍(2021)运用动态规划原理求得最优策略和值函数满足的HJB方程,得到了最优停止再保险-投资策略和值函数的显示解。以终端效用为目标,Liang,Bai和Guo(2011)分别研究了当保险公司赔付过程满足传统经典风险模型和扩散逼近风险模型时再保险策略选择问题。
同样在扩散风险模型下,为实现预期折现收益最大化,Højgaard和Taksar(1998)也做了相关研究,并给出了相应的数值模拟结果进行分析。Brachetta和Schmidli(2020)则对比了不同的再保险种类,分别求解比例再保险和超额损失再保险SAHARA效用函数最大化的再保险策略。Li和Liu(2015)则假设在马尔科夫控制环境下,保险公司满足跳-扩散风险模型,求得了保险公司的最优投资和CARA效用函数最优策略的显式解。值得注意的是,与一般的财富过程模型相比,跳-扩散风险模型更接近保险公司实际的赔付过程。Liu等(2021)考虑了将鞅方法应用于由Lévy过程驱动的模型,研究了追求效用最大化下最优投资-比例再保险策略。
..................................
第三章 破产概率目标下再保险策略选择博弈..................... 10
第一节 保险公司和再保险公司的风险模型........................ 10
第二节 再保险策略选择博弈.......................... 13
第四章 期望终端盈余效用最大化下再保险策略选择博弈..................... 28
第一节 考虑投资的再保险策略选择博弈模型............................ 28
第二节 投资策略与再保险选择策略博弈........................... 30
第五章 总结与展望............................ 5
第一节 研究结论................................ 53
第二节 研究展望................................ 54
第四章 期望终端盈余效用最大化下再保险策略选择博弈
第一节 结果比较与灵敏性分析
下面,分别探讨不同博弈情况下模型主要参数对再保险合约双方效用损益的影响。除特别说明,各模型参数取值参照表4-1,其大小比例与实际情况较为接近。

金融论文参考
............................
第五章 总结与展望
第一节 研究结论
本文对再保险过程中,保险公司与再保险公司选择怎样的再保险策略进行了讨论。作为参与再保险合约的不同主体,其目标都是追求自身利益最大化。保险公司与再保险公司对于是否分保以及分保的比例和再保费都有着决定权。保险公司可以根据再保险价格与风险状况决定比例再保险的购买与否及购买数量,同时再保险公司也可根据再保险价格与风险状况决定承保与否。在扩散风险模型下,不考虑投资时,双方都以破产概率最小为目标,首先给出两公司的风险模型、相应的目标函数。然后,利用最优化理论得到不同博弈情形下的最优比例再保险策略。在再保险合约双方都可以投资风险资产的情况下,考虑了再保险合约双方的比例再保险策略选择博弈问题。假设两公司都具有指数效用函数,运用动态规划原理,建立并求解相应的HJB方程,得到了不同博弈情形下再保险合约双方的最优投资策略、比例再保险策略和值函数的显示解,以及再保险合约成交时再保费满足的条件。本文得到的主要结论如下: 在扩散风险模型下,不考虑投资,以破产概率减小为目标,主要结果如下:
1. 保险公司主导。因再保费的支出以及自身保费收入的变化会影响保险公司的分保意愿,保险公司的最优自留比例随着再保费的增大而增大,随着自身保费收入的增大而减小。因保险公司的财富过程会影响其破产概率,所以保险公司的破产概率随着再保费的增大而减大,随着自身保费收入的增大而减小,同时随着自身风险的增大而增大。当保险公司波动率变大时,再保险公司为确保破产概率不大于初始经营情况,其收取的最低再保费将上升。
2. 两公司共同主导。当保险公司自身收入增加时,其拥有更多财富用于购买再保险,因此最优再保费增加。而当保险公司波动率增加时,再保险公司为维持经营,收取再保费的价格将会上升。再保险公司自身收入增加时,再保险合约双方的破产概率收益均会减小。再保险公司的破产概率损益随着保险公司波动率的增加而减小。当再保险公司自身风险升高时,其需要降低再保费以承保更多保险公司业务,来降低公司整体风险,因此最优再保费减小。
参考文献(略)
