本文是一篇金融论文研究,本文分别利用Hurst指数与移动Hurst指数计算近5年的中国证券市场的平均周期以及提供市场择时策略.本文基于具有周期解的SIR模型对市场股本流动进行建模,并采用贝叶斯正则化神经网络估计了模型的参数.
第一章绪论
1.1研究背景和现状
行为金融学理论[1]与分形市场理论是随着对传统金融学理论[2]的不断挑战而发展起来的.1936年,经济学家凯恩斯提出的股市"选美竞赛理论"和"空中阁楼理论"首次强调了心理预期在投资决策中的作用;20世纪80年代中期以后,国外学者们将逐渐发展起来的行为金融学理论与金融市场的实践相结合并进行研究,芝加哥大学的Thaler与耶鲁大学的Shiller成为了该领域的杰出代表;到了20世纪90年代,行为金融学理论得到了进一步的发展.与此同时,美国一位著名投资基金研究部负责人Edgar E.Peters[3,4]提出将"分形几何学"与"混沌理论"应用于资本市场的研究,并先后出版了Fractal Market Analysis:Applying ChaosTheory to Investment and Economics以及Chaos and Order in the Capital Markets:ANew View of Cycles,Prices,and Market Volatility两本书籍,系统地阐述了两个观点:1.资本市场是一个非线性动力系统;2.资本市场具有分形结构.因此,分形理论可以用于资本市场的研究.近年来,国外学者发表的关于行为金融学研究的文章层出不穷.2019年,Ahmed Bouteska[5]发表的Psychology and behavioralfinance:Anchoring bias byfinancial analysts on the Tunisian stock market一文中定量地检测了突尼斯股票市场上金融分析师中锚定偏差行为的存在;2021年,VasileiouEvangelos[6]在Behavioralfinance and market efficiency in the time of the COVID-19pandemic:does fear drive the market?一文中利用恒定增长模型,基于Google指数的行为模型,研究了COVID-19爆发期间美国股票市场的效率,证明了恐惧情绪对美国股票的表现产生了负面影响.
...........................
1.2研究内容和创新
本文主要的研究内容是将行为金融学理论与分形市场理论相结合应用于中国证券市场的研究.基于行为金融学理论,我们可以认为中国证券市场上的投资行为是存在行为传染的;基于分形市场理论,我们可以认为中国证券市场具有分形结构且具有平均周期.本文选取近5年的上证50指数的收盘价序列作为样本数据.首先,本文利用Hurst指数计算中国证券市场的平均周期,利用移动Hurst指数判断市场反转点并提供市场择时策略.然后,本文基于具有周期解的SIR模型对中国证券市场的股本流动建模:将传染率改为周期函数与计算出的市场平均周期相结合.最后,本文采用贝叶斯正则化神经网络估计模型参数,具体做法是将模型的数值模拟结果作为网络的训练样本;将从市场中获取的真实数据作为网络输入来估计模型参数.最终结果是近5年的中国证券市场的平均周期约为400个交易日.模型的参数估计的结果在合理范围内.以上结果证明了中国证券市场上的投资行为存在周期性的传染,这种周期性的传染导致了市场的平均周期的存在;同时,市场的平均周期的存在也导致了投资行为的周期性的传染.
本文的创新之处:
1.本文利用Hurst指数计算出了中国证券市场近5年的平均周期,利用移动Hurst指数判断出了市场反转点并且提供了择时策略;
2.本文基于具有周期解的SIR模型对中国证券市场的股本流动进行了建模:将传染率改为周期函数的形式与计算出的中国证券市场的平均周期相结合;
3.本文采用贝叶斯正则化神经网络估计了模型的参数,估计结果在合理的范围之内.
............................
第二章中国证券市场的分形结构及行为传染
2.1分形理论在中国证券市场中的应用
目前,分形理论[10–12]中对于"分形"并没有给出一个明确的定义.分形是一种具有以下特性的结构:自相似性[13]、整体确定性、局部随机性.其中,自相似性指的是局部与整体具有相似性;整体确定性与局部随机性可以理解为:分形是由一个确定的简单的规则而产生的无限复杂的结构.分形可以分为有规分形和无规分形,有规分形是指具有具体且严格的自相似性的分形,它可以由递归产生,而无规分形是指具有统计意义上的自相似性的分形,它可以由迭代产生.典型的有规分形有:Julia集、Mendelbrot集等,如下图所示:
金融论文怎么写
.............................
2.2行为金融学理论在中国证券市场中的应用
行为金融学理论打破了传统金融学理论中的关于"理性投资者"[14,15]的假设.在行为金融学理论框架下,投资者是非理性的,且投资行为会相互传染.这种投资行为的传染类似于疾病的传染,一但不受控制地传染下去,资本市场就会出现"追涨杀跌"等市场异象.这些异象用传统的金融学理论是无法解释的.
20世纪80年代以来,资本市场行为传染即羊群效应[16–19]的研究受到了越来越多的重视.羊群效应本是指动物的一种群体觅食,移动的行为,将其应用于资本市场的研究中,反应的是投资者之间投资行为相互传染的现象.具体是指投资者在做出投资决策时忽略自己对信息价值的判断而选择跟随大部分投资者的选择.这是一种非理性的投资行为.研究表明正是这种行为导致了市场的异常波动.
国内的一些学者也纷纷开始研究中国证券市场中是否存在行为传染.湖南大学的袁瑜[20]利用CCK模型验证了中国股市中存在行为传染;东北财经大学的王春丽、白红丽[21]利用ARCH模型对2006年至2011年中国股市进行的实证分析结果表明:行为传染在中国股市剧烈震荡过程中依然显著存在,深圳证券市场比上海证券市场更加严重,股票上涨阶段的行为传染比下跌阶段更为显著;上海理工大学的冯伟[22]运用二次函数型、指数函数型、对数函数型和幂函数型四种不同方法同时建立模型,以沪深300指数样本股票为研究对象,采用CSAD法并运用时间序列中的GARCH模型建模,对中国证券市场的行为传染进行了对比实证研究,得出中国证券市场存在行为传染的结论.
...................................
第三章股本流动模型..........................6
3.1经典的SIR模型...................................6
3.2股本流动模型.....................................7
第四章中国证券市场平均周期的计算.......................11
4.1 Hurst指数及重标极差法.........................11
4.2平均周期的计算..........................12
4.3移动Hurst指数...........................15
第五章股本流动模型的参数估计....................17
5.1贝叶斯正则化神经网络................................17
5.1.1 BP神经网络............................17
5.1.2贝叶斯及正则化方法.............................18
第五章股本流动模型的参数估计
5.1贝叶斯正则化神经网络
贝叶斯正则化神经网络是在传统的BP神经网络的基础上加入了贝叶斯以及正则化方法形成的一种新的网络结构.
5.1.1 BP神经网络
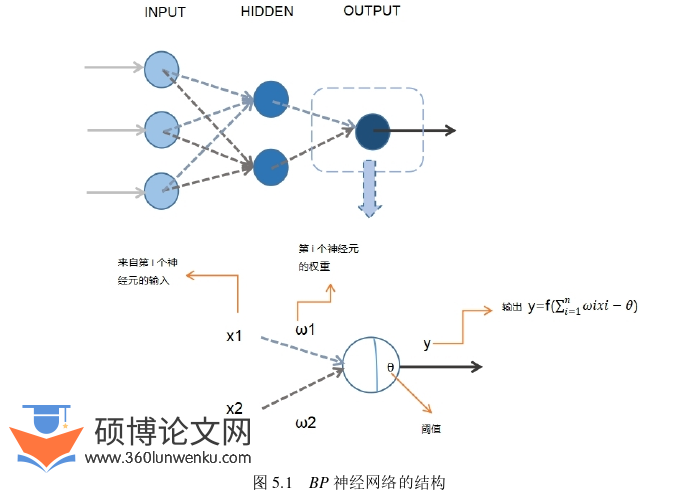
BP神经网络[30]是一种多层前馈神经网络,网络的主要特点是信号前向传递,误差反向传播.网络的训练过程中信号先进行前向传播,信号进入输入层经过隐含层的处理进入输出层,如果输出层未得到期望的输出则进入反向传播,根据代价函数不断调整网络的权重和阈值,直至代价函数达到最小值.BP神经网络的结构如下图所示:
金融论文参考
................................
第六章总结与展望
本文主要的创新之处是将行为金融学理论与分形市场理论结合应用于中国证券市场的研究.本文分别利用Hurst指数与移动Hurst指数计算近5年的中国证券市场的平均周期以及提供市场择时策略.本文基于具有周期解的SIR模型对市场股本流动进行建模,并采用贝叶斯正则化神经网络估计了模型的参数.
1.本文基于具有周期解的SIR模型建立的股本流动模型有效地结合了中国证券市场的平均周期与投资行为的传染,证明了中国证券市场上的投资行为存在周期性的传染,这种周期性的传染导致了市场的平均周期的存在;同时,市场的平均周期的存在也导致了投资行为的周期性的传染;
2.本文采用贝叶斯正则化神经网络估计了模型的参数,但是网络的训练数据只包含了108组数据,网络结构较简单.
本文今后的研究方向:
1.在股本流动模型中可以加入时滞项,同时,尝试增加R仓室到S仓室的流动;
2.在ode45函数求解的过程中,尝试找到自动更新参数并输出结果的方法;
3.用非参数估计的方法确定传染率函数的具体形式.
参考文献(略)
