1 绪论
1.1 研究背景与意义
以化石能源消耗为主的能源体系结构不仅影响着全球生态环境,也对人类的生存造成严重威胁[1],而化石能源日益枯竭[2],因此,必须加快新能源开发利用的步伐。潮汐能是一种能量密度大、可准确预测、规律性变化且低耗能的可再生能源,它清洁无污染、不受洪枯水期的影响,分布广泛[3,4],开发潜力巨大。目前的潮汐电站机组采用定转速运行方式,但由于电站水头呈周期性变化,且变幅很大,导致机组工况频繁转换,大多时间均运行于非最优工况,造成机组运行效率低、振动和磨损严重等问题,严重影响了潮汐电站的发展,可变速机组能根据水头和负荷变化调整机组转速使其运行于高效率区,进而提高机组运行效率,改善运行工况。
可变速技术的实现有两种方式:采用双馈电机或全功率变流器实现机组变速,相比于采用双馈电机的可变速机组,采用全功率变流器的可变速机组有以下优点:(1)启动过程较简单,可避免多级机械传动造成的额外损耗、噪声以及可靠性降低等问题;(2)全功率变流器将机组和电网隔离,两者间的影响减小,机组转速范围更广,可实现转速的完全调节[5];(3)机组低电压穿越能力更强。同时,随着电力电子器件的快速发展,采用全功率变流器实现机组变速运行的技术受到了广泛关注,但目前该技术主要应用于风电及部分抽蓄机组中[6-9],并未用于水头变化频繁、变幅较大的潮汐电站,而我国潮汐电站机组容量普遍偏小,可采用全功率变流器实现机组变速运行,从而提高潮汐发电机组运行效率、改善运行工况,因此,本文将在分析可变速永磁同步全功率变流潮汐发电系统运行原理及其控制策略的基础上,建立可变速潮汐发电系统仿真模型,通过仿真分析验证模型和控制策略的正确性,其次由于机组的电磁暂态模型较为复杂,仿真计算时间长,为了更好地研究水轮机系统和提高仿真效率,本文对所建立的系统模型进行简化来减小系统仿真时间。
........................
1.2 国内外研究进展
1.2.1 潮汐电站的发展现状
11 世纪的潮汐磨坊是最早的潮汐能利用方式,潮汐电站的开发利用则始于1912 年德国胡苏姆兴建的一座 5kW 潮汐电站,随后世界各国都进行了潮汐电站的开发利用,且技术逐渐走向成熟化,开发规模逐渐趋于大型化,1966 年法国建成了装机 24 万 kW 的朗斯潮汐电站,年发电量可达 5.44 亿 kWh,是当时世界上最大的潮汐电站,其五十多年的成功运行证实了潮汐发电技术的可行性。此外,世界上还有许多大型潮汐电站处于规划或建设阶段,如俄罗斯美晋电站设计容量为 1500 万 kW;英国塞汶电站为 720 万 kW;加拿大芬地湾电站为 380 万 kW,按目前潮汐电站的发展速度,预计到 2030 年,全世界潮汐能年发电量可高达 600亿 kWh[10]。
我国潮汐能理论储量约为 1.1 亿 kW,可开发装机容量为 2179 万 kW,年发电量可达 624 亿 kWh,主要集中在福建、浙江、江苏等沿海省区[11]。我国在潮汐能利用方面是起步较早,在 1950 年便开始利用潮汐能驱动水轮泵站[12],但潮汐电站的开发始于 50 年代后期,至 1958 年,共建成了潮汐电站 40 多座,70 年代又建成了 10 余座,可由于电站经营困难等原因,多数潮汐电站已被弃用[13],截至 2011 年,我国仍在运行的潮汐电站仅有 8 座,这 8 座潮汐电站总装机6120kW,其中,江厦电站装机容量为 4100kW,超过总装机容量的 1/2[13,14],是我国潮汐电站的典范,它的长期成功运行为我国潮汐电站的开发利用积累了宝贵经验。总体来看,我国对潮汐能的开发力度明显不足,但随着诸多潮汐电站的成功运行经验的积累以及发电技术的长足进步,我国的潮汐电站已从原来的“能发电”逐渐转变为如今的“稳定发电”,这对我国进一步大规模开展潮汐电站的商业化应用提供了有力支撑,近年来,我国越来越重视潮汐能等海洋能发电技术的开发利用,并计划到 2020 年全国海洋能总装机容量达到 5 万 kW,促使海洋能发电技术实现稳定发电,形成海洋能发电产业链,在这样的规划之下,潮汐发电行业将迎来较好的发展前景[15-17]。
.......................
2 可变速潮汐发电机组及变流器数学模型
2.1 引水系统及非线性水轮机数学模型
2.1.1 非线性水轮机数学模型
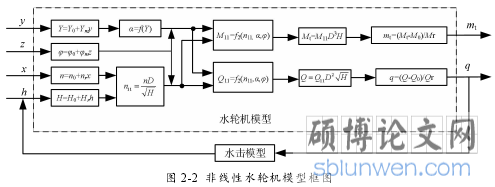
对于水轮机模型的建立,学者常常采用的是线性水轮机模型,这种水轮机模型在额定工况点或者小扰动时,一般可以达到建模要求。但由于潮汐电站水头变幅较大,机组的运行工况比较多,水轮机非线性特征比较明显,显然,线性模型不符合潮汐发电系统的建模要求,因此本文需建立非线性水轮机模型。
针对水轮机的非线性建模,目前应用较多的方法是以模型综合特性试验曲线为基础,利用水轮机特性数表来表达水轮机的非线性特性[49]。
2.2 永磁同步发电机数学模型
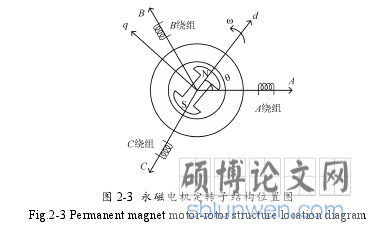
如图 2-3 所示是永磁同步电机定、转子结构位置图,中间标有 N、S 极的为转子,上面装有永磁体,A 、B、C 三相绕组装在发电机定子上,将A 轴作为转子的参考位置, 是永磁体偏离A 相轴线的角度,永磁体的磁链方向为图中所示d轴,q轴超前d轴 90°[51]。
3 可变速潮汐发电系统控制及其建模..........................21
3.1 水轮机控制系统...........................................21
3.1.1 最优转速发生器.......................................22
3.1.2 转速调节系统................................23
4 可变速潮汐发电系统仿真与分析..................................35
4.1 水轮机及其控制系统仿真模型.......................................35
4.1.1 引水系统及非线性水轮机仿真模型............................35
4.1.2 最优转速发生器仿真模型............................36
5 可变速潮汐发电机控制及变流器简化与参数整定..........................49
5.1 可变速潮汐发电机控制及变流器简化数学模型...........52
5.2 可变速潮汐发电机控制及变流器简化仿真模型....................52
5 可变速潮汐发电机控制及变流器简化与参数整定
5.1 可变速潮汐发电机控制及变流器简化数学模型
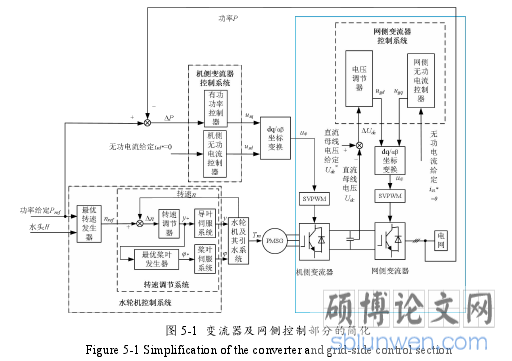
整个可变速潮汐发电系统中仿真耗时长的元件是变流器中的电力电子元件,其制约了仿真步长的提高,精细模型的仿真步长使得数据的记录、计算、存储量都大幅度增加[56]。4.7.1 和 4.7.2 节仿真分析表明,在功率扰动时直流母线电压值保持稳定状态,说明网侧变流器可以快速稳定并将机侧变流器输出的功率送入电网,因此可以忽略电容和网侧变流器的动态过程;4.8 节仿真结果表明,变流器等电力电子元件的响应时间一般在毫秒级,远远小于水轮机调速系统的秒级,且能快速稳定,因此,在对水轮机调速系统进行研究时,可以忽略变流器等电力电子元件的动态过程,专注研究水轮机及发电机侧相关量的变化情况,这样既可以有效的简化模型,减少仿真时长,又能够很好的保留水轮机调速系统的特性。因此可忽略图 5-1 蓝色方框部分。
6 结论与展望
6.1 结论
为解决潮汐电站水头变化幅度大引起的机组运行于非最优工况运行时间长、运行效率低以及振动、磨损等问题,本文提出全功率变流的可变速永磁同步潮汐发电系统,并对其数学模型、控制策略、模型仿真及简化做了相应的研究,研究成果如下:
(1)分析了可变速潮汐发电系统的基本结构及运行原理,推导了可变速永磁同步全功率变流潮汐发电系统控制对象的数学模型,包括非线性水轮机、永磁同步电机、机侧变流器和网侧变流器的数学模型。
(2)分别提出了水轮机、机侧变流器、网侧变流器的控制策略:对机组转速调节器采用 PID 控制,对发电机侧变流器采用转子磁场定向矢量控制以控制机组输出有功、无功功率,对电网侧变流器采用电网电压定向矢量控制以实现直流母线电压的稳定。
(3)基于 Matlab/Simulink 软件,建立了可变速永磁同步全功率变流潮汐发电系统仿真模型,仿真分析了功率给定增加和减小时系统各相关量的变化情况,结果显示:机组可通过转子动能的储存和释放快速响应功率指令,转速可随功率和水头变化调整为对应的最优转速,机侧变流器和网侧变流器能准确控制其有功、无功功率的输出,可有效维持直流母线电压稳定,表明所建模型可准确反映系统动态特征,验证了模型的正确性和控制策略的可行性。
(4)由于变流器和水轮机仿真步长不一致,导致精细模型仿真时间较长,而变流器等电力电子元件能快速稳定,因此,在忽略电容和网侧变流器的动态过程的基础上,对发电机控制和变流器部分进行了简化,对比了精细模型与简化模型的仿真结果,结果表明:简化模型与精细模型有着基本一致的动态过程,验证了简化模型的正确性;精细模型仿真步长为 5×10-6s,仿真时长为 3.0703h,简化模型仿真步长为 1×10-3s,仿真时长仅为 53.93s,表明简化模型可显著减少仿真时长,为可变速潮汐发电机组的仿真研究节省了时间;此外,对横田浩推荐公式和由综合主导极点配置所得的整定公式进行仿真结果对比,验证了由综合主导极点配置所得的参数为最优 PID 参数。
参考文献(略)
