1 绪论
1.1 研究背景及意义
目前,地震对人类的威胁不断增大,成为最为严重的自然灾害之一。伴随地震所释放出来的能量往往会对建筑(构筑)物产生严重的损害;破坏道路、地面,造成地面局部区域出现裂缝、坍塌;在某些山坡部分出现大面积滑坡、泥石流甚至会引发雪崩,引起海底河床运动进而引发海啸等其他灾害发生。地震在中国主要表现出震源较浅、强度及频率都较高的特点。中国的地理位置较为特殊,受多个板块挤压,地震带发育特别厉害。
自改革开放以来,我国发生的地震灾害很多,遍布我国各个省市。随着人与自然矛盾的激化,地震灾害在近二年发生的频率不断提高,严重威胁了人们的生命财产安全。从二十世纪以来,据有关数据显示,我国竟然有超过五十五万的人死于地震,占比超过全球地震总死亡人数的二分之一。自我国成立以来,近百次的地震使我国二十多个省份受到不同程度的破坏,东部地区受灾面积更大、范围更广,地震中死亡人数高达二十七万,占全国灾害死亡人数的百分之五十四。近年来伴随城市化进程的加快,地震这种自然灾害严重威胁了人民的生命、财产安全。因此,防震减灾工作显得尤为重要并发展成为了一个重要课题。
........................
1.2 场地地震反应研究现状
场地地震作用下的动力反应分析一直是工程抗震领域比较活跃的研究方向。不论是高大建筑物的选址,还是工程场地安全性评价分析,都离不开地震反应分析。在研究该问题时,通常将场地简化为一个下部为基岩、上部为均匀层状介质的土体。震源处产生的地震波透过基岩传播至场地表面,通过分析地震波入射后地表的响应及场地运动特性,从而为工程抗震提供指导。地震波从震源传播至近地场,由于传播距离较大,一般认为地震波是一组相互平行的体波透过基岩作用至近地场。地震作用下的场地反应课题在过去几十年取得了许多的理论成果。目前对该问题的研究主要有:数值模拟分析法和理论研究法。下面简单对这些方法及研究成果进行简单的回顾。
1.2.1 数值模拟分析方法
在许多有关地学领域的物理问题研究中,通过数学物理方法基本确定了这些问题的定解条件和基本方程,但是能用解析法求解的只是少数的较为简单的问题。对于绝大多数问题,由于实际情况较为复杂,所得的方程存在非线性性质的情况,往往不能求得精确解。处理该问题主要有以下方法。其一是将方程的边界条件简化,得到简化情况下的解析解。这种方法简化太多可能会使计算结果误差较大甚至出现错误。为此人们探索和发展了另外一种能够较好解决这种问题的方法-数值模拟方法。
地震数值模拟方法能够有效解决解析方法求解过程困难的问题,为人们研究复杂场地的动力响应问题提供了便利。目前,科学技术的不断发展和地震波理论实际应用的不断广泛,地震波数值模拟技术也得到了飞速的发展,形成了以下几种较为成熟的数值模拟技术,其中包含了积分方程法、射线追踪法和数值解析法等。
积分方程法是建立在波动方程的积分表达基础上的一种方法。Bakamjian[1]首先将边界积分方程法的思想应用于地震波的数值模拟中,符力耘和牟永光[2]用弹性波边界元法实现了二维和三维问题的弹性波正演模拟。其次,符力耘等[3]谈到了非线性 Fredholm 积分方程的正演问题,之后符力耘[4]又给出了含起伏地表的广义 Lipmann-Schwinger 积分方程的数值模拟方法。
.......................
2 地震波理论基础
2.1 弹性波动方程
弹性波动方程是研究地震波传播以及运动规律的基础。在弹性波理论中,通常把物体的性质分为均匀性和非均匀性。在非均匀介质中,将弹性介质相同的点连成一个区域,可将介质相同的区域看作均匀的,整个非均匀介质可分为很多个均匀的区域,这就是我们通常所说的层状模型,用来研究地震波的传播。本节将以均匀介质为例,依照弹性力学中的应力应变关系,从而推求弹性波的波动方程。
2.1.1 弹性力学的基本假定
地震波在基岩中的传播可将其视作弹性波的传播过程,弹性波的传播是以弹性理论作为基础,弹性理论是建立在以下几点基本假设之上。地震波在基岩中的传播可将其视作弹性波的传播过程,其传播基于弹性力学理论,前提有以下几点假设。
弹性波动方程是研究地震波传播以及运动规律的基础。在弹性波理论中,通常把物体的性质分为均匀性和非均匀性。在非均匀介质中,将弹性介质相同的点连成一个区域,可将介质相同的区域看作均匀的,整个非均匀介质可分为很多个均匀的区域,这就是我们通常所说的层状模型,用来研究地震波的传播。本节将以均匀介质为例,依照弹性力学中的应力应变关系,从而推求弹性波的波动方程。
2.1.1 弹性力学的基本假定
地震波在基岩中的传播可将其视作弹性波的传播过程,弹性波的传播是以弹性理论作为基础,弹性理论是建立在以下几点基本假设之上。地震波在基岩中的传播可将其视作弹性波的传播过程,其传播基于弹性力学理论,前提有以下几点假设。
(1)连续性。假设物体是被介质完全填满。实际的物体都是由分子、原子等微粒组成,严格地讲,这不符合连续性假设。但是从宏观上看,应力大小与物体几何尺寸相比,依然满足假设。
(2)完全弹性。假设构成物体介质是完全弹性介质。物体的应力应变满足胡克定律,弹性常数与受力历史无关。
(3)均匀性。假设物体的介质是由同一种材料构成。任意一点的研究结果可以适用于全部物体。
(4)各向同性。假设在构成物质的各个方向上,介质性质相同。方向不会对研究结果产生影响。
3 斜入射 SH 地震波作用下的场地效应........................... 14(4)各向同性。假设在构成物质的各个方向上,介质性质相同。方向不会对研究结果产生影响。
(5)小变形。假设物体的变形都极小。与物体原来的几何尺寸相比,各点的弹性位移特别小。在计算时可将应变的二次幂及更高次幂进行忽略,使方程式简化为线性方程,因而可以用叠加原理,还可以按照变形前的尺寸来计算问题。
理想弹性体均满足前四点假设。地震波理论主要限于理想弹性体的小变形问题。实际地层介质模型更为复杂,在此以弹性介质进行研究可大大简化问题的难度。
..........................理想弹性体均满足前四点假设。地震波理论主要限于理想弹性体的小变形问题。实际地层介质模型更为复杂,在此以弹性介质进行研究可大大简化问题的难度。
2.2 关于地震波传播的讨论
几何地震学对是地震波波前的空间位置与其传播时间的关系进行研究。该学科是通过引用波前、射线等几何图形对波的运动过程及其规律进行研究,我们又将其称为地震波的运动学。它是研究地震场地响应的重要理论,下面就分别从不同的方面对该部分进行介绍。
2.2.1 地震波传播的基本原理
波是由一系列的质点振动形成的波动并且以一定的速度沿某一方向向前传播,波动伴随着能量的传播。
a.惠更斯-菲涅尔原理
惠更斯原理是指波传播到的各点均可看做形成新的子波的波源,并在任意时间后,这些子波形成的行的包络面就是新的波前。可以用它来计算波前到达介质中任一点的时间。
惠更斯-菲涅尔原理是一种用来构制下一时刻波前面位置的几何方法。应用该原理可构制反射界面和折射界面等。波射线的方向在不同介质中方向不同,均匀介质中为直线,非均匀介质为曲线且垂直分界面。
几何地震学对是地震波波前的空间位置与其传播时间的关系进行研究。该学科是通过引用波前、射线等几何图形对波的运动过程及其规律进行研究,我们又将其称为地震波的运动学。它是研究地震场地响应的重要理论,下面就分别从不同的方面对该部分进行介绍。
2.2.1 地震波传播的基本原理
波是由一系列的质点振动形成的波动并且以一定的速度沿某一方向向前传播,波动伴随着能量的传播。
a.惠更斯-菲涅尔原理
惠更斯原理是指波传播到的各点均可看做形成新的子波的波源,并在任意时间后,这些子波形成的行的包络面就是新的波前。可以用它来计算波前到达介质中任一点的时间。
惠更斯-菲涅尔原理是一种用来构制下一时刻波前面位置的几何方法。应用该原理可构制反射界面和折射界面等。波射线的方向在不同介质中方向不同,均匀介质中为直线,非均匀介质为曲线且垂直分界面。
b.费马原理
费马原理是几何地震学特别重要的定理之一。在几何地震学中,时间场是通过波射线和波前面来表示的,波射线传播方向始终与波前垂直。费马原理主要指的是波沿着垂直波前方向传播且沿该方向传播旅行时间最短。c.互换原理
d.叠加原理
叠加原理指的是不同地震波在空间中某一点相遇,再相遇点质点的震动为各个分震动之和,该点的位移为各个分震动在该处的矢量和。换句话就是每条波在传播的过程中都是独立的进行传播,对叠加点贡献自己的一份力量,这种特性称之为叠加原理。
...........................
费马原理是几何地震学特别重要的定理之一。在几何地震学中,时间场是通过波射线和波前面来表示的,波射线传播方向始终与波前垂直。费马原理主要指的是波沿着垂直波前方向传播且沿该方向传播旅行时间最短。c.互换原理
d.叠加原理
叠加原理指的是不同地震波在空间中某一点相遇,再相遇点质点的震动为各个分震动之和,该点的位移为各个分震动在该处的矢量和。换句话就是每条波在传播的过程中都是独立的进行传播,对叠加点贡献自己的一份力量,这种特性称之为叠加原理。
...........................
3.1 斜入射 SH 波产生的反射和透射................................. 14
3.1.1 SH 波在弹性分界面处的反射和透射.......................... 14
3.1.2 SH 波在弹性分界面处的折射........................ 16
4 斜入射地震 P 波作用下的场地效应..................................27
4.1 斜入射 P 波在分解面处的反射和透射.................................27
4.1.1 P 波在自由表面上的反射...........................27
4.1.2 P 波在弹性分界面处的反射和透射..............................29
5 斜入射 SV 地震波作用下的场地效应............................46
5.1 斜入射 SV 波在分界面处的反射和透射..............................46
5.1.1 SV 波在自由表面处的反射.......................46
5.1.2 SV 波在弹性分界面处的反射和透射..........................48
6 三维斜入射地震波共同作用下的场地效应
6.1 三维地震波斜入射计算方法
6.1.1 三分量地震波入射时空间关系
前文已经对地表任意观测点的地震动响应进行了讨论分析,分别得出了 P、SH、SV波不同角度入射情况下,地表观测点的响应地震动时程。现按照等时振幅叠加原理,对地表观测点的三维地震动进行合成,最终得到地表观测点的实际震动情况。
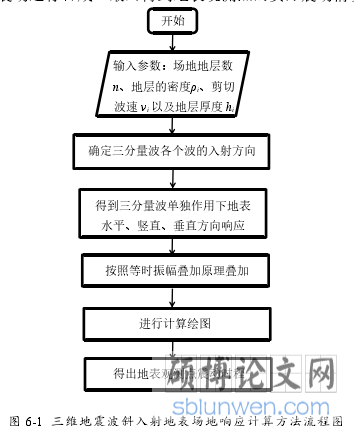
由于纵横波引起质点振动方向与其传播方向存在差异。横波又被分为 SH 波和 SV 波,这两个波引起质点的震动将会互相垂直且都垂直纵波的传播方向。在基岩处发射的地震波必然存在一定的空间关系。本文取以下空间关系进行分析研究。在空间直角坐标系中认为P 波沿着 x 轴方向传播,SH 波沿着垂直于纸面的 y 轴方向传播,SV 波沿着 z 轴方向传播,且它们两两互相垂直。
.......................7 结论与展望
7.1 结论
目前,对斜入射三维地震波作用下的场地响应问题的研究较少,通常研究其某一分量对场地或建筑的动力响应。本文建立了三维地震波入射弹性均匀场地模型,基于地震学基本原理与弹性力学基本假设,按照地震动合成原理,首先研究了 SH、P、SV 地震波独自作用下均匀场地的地震相应问题,并对影响其地表响应的因素进行了探究分析。其次提出了斜入射三维地震波共同作用下均匀场地地震响应研究方法,即等时震动叠加方法。最后分析了不同入射角度、不同上覆土层厚度两种因素对地表场地响应的影响。得到以下几点结论:
(1)均匀场地 SH 波入射情况下,随着入射角的增大,地表响应振幅逐渐减小,尾振减小,地震动持时变短。入射角小于 60°时,地表现出位移加倍;地层厚度主要对地震波抵达观测点的传播时间影响较大,表现为随地层厚度增大最大地表响应振幅出现时间后移。
(2)均匀场地 P 波入射情况下,随着入射角的增大,水平方向地表最大振幅震动逐渐增强,竖向最大响应振幅逐渐减小,且最大响应振幅为入射波振幅的 3 倍,地表旋转震动特性逐渐增强。地震动持时、尾振均随入射角增大略有减小。随着地层厚度的增大,水平方向地表最大振幅逐渐减小,一旦上覆土层厚度超过基岩计算厚度,最大振幅约为 1.5倍振幅保持不变;竖直方向地表最大振幅呈现增加的趋势,地震动持时和尾振随地层厚度增加呈现出增加的趋势。
(3)均匀场地 SV 波入射情况下,随着入射角的增大,水平和竖直方向震动均出现先增强后减弱的趋势。但当入射角约为 36°接近临界角时,水平方向震动突增到入射振幅的 3 倍。地震动持时呈现出减小的趋势。随着上覆土层厚度增加,水平方向的地震动时程随着上覆土层厚度的增加呈现出增加的趋势,竖直方向最大响应振幅呈现出先增大后减小的趋势。
参考文献(略)
