1 绪论
1.1 研究背景
1.1.1 人工神经网络发展历史
人工神经网络(Artificial Neural Networks, ANNs)是由人工方式构造的非线性动力学网络系统, 由大量的处理元件连接而成, 是对人脑神经系统的结构和功能的模拟. 它的主要特点有: 快速的信息处理能力、非线性全局作用、鲁棒性、并行性、联想记忆能力等. 目前人工神经网络用于传感技术与机器人、自适应滤波、语音识别等诸多领域.
最早的基于生物神经元工作原理而构建的数学模型被简称为M-P模型, 它是由心理学家 McCulloch 和数学家 Pitts 于 1943 年提出的[1]. MP 神经元模型描述了人工神经元具有多输入单输出结构, 可以完成简单的、有限次的逻辑运算.
心理学家 Hebb 对突触的可塑性机制进行了研究, 认为突触前神经元向后神经元持续重复刺激, 可增加其传递效能. 1949 年 Hebb 提出了这一学习规则, 它是一种典型的无教师学习(也叫无监督学习)规则[2].
第一个在实际中得到应用的神经网络——感知机(Perceptron) 模型于1958年问世[3], 该模型是由计算科学家 Frank Rosenblatt 所提出的, 是一个结构为 n-1(n>1) 的两层神经网络. 理论上已经证明, 对于线性可分样本, 感知机可以在有限时间内对其正确分类.
自适应线性元件 Adaline 是由电机工程师 Widrow 和 Hoff 于 1962 年提出的, 该线性网络是连续取值的模型, 可用于抵消通信中的回波和噪声.
1969 年, 计算机科学家 S. Minsky 和 S. Papert 出版了《感知机》专著[4], 书中论证了单层感知机只能进行线性分类, 对线性不可分的问题, 即便是非常简单的“异或”问题, 单层感知机也无力解决. 他们还指出, 找到一个训练多层网络的算法并非易事. 受此影响, 一些从事神经网络研究的学者对本学科的发展前景失去信心, 人工神经网络的研究开始陷入“低谷”.
著名的误差反向传播(Backpropagation, BP)算法是 1974 年由哈佛大学的 Werbos 在其博士论文中最先提出来的, 用于训练多层神经网络[5]. 可惜的是, 他的工作在将近十年的时间里, 都没有被正确的认识并对其做进一步的研究.
...............................
1.2 国内外相关工作研究进展
1.2.1 PCA 算法近年来的研究进展
近年来, 针对前几个最大特征值所对应的主分量(Principal component, PC)或主子空间(Principal subspace, PS), 以及几个最小特征值对应的次分量(Minor component, MC)或噪声子空间(Minor subspace, MS)均被深入研究. 当需要实时在线提取主/次分量时, 开始时学习率选大一些值, 然后再逐渐减小, 通常这样做较为有效.
2016 年, Shamir 分析了子空间在线 PCA 学习算法[45], 首次得到了提取前 k(k ≥1) 个主分量的收敛性结果, 但是该算法只是局部收敛, 初始矩阵需要一个比较精确的条件. 当 k =1时, 该算法即为 Oja 学习算法.
2017 年, 朱泽园探讨了一种更快的子空间在线 PCA 方法[46]. 假设 Σ是由独立同分布, 且分布未知的在线 d 维输入向量 x 所构成的 d d×维协方差矩阵, 则朱方法指的是在O(dk) 空间下, 近似逼近协方差矩阵 Σ 的前 k(k ≥1) 个特征向量, 并在随机赋初始权值的条件下, 证明了 Oja 学习算法的全局收敛性. 另外第一次展示了具有无间隙的(gap-free)特征, 即收敛速度与逼近误差成正比而且与特征间隙独立.
2018年, Li等人把在线PCA转化为一个随机非凸优化问题[47], 首次证明了在线PCA算法的近似最优有限样本误差界. 在次高斯分布的假设下, 证明了有限的样本误差界与极大极小信息下界非常接近.
近年来, PCA 的研究从线性学习算法扩展到非线性学习算法. Schölkopf(1997)应用核函数的核主成分分析(Kernel Principal Component Analysis, KPCA)可以捕捉非线性数据结构[48], 被应用到人脸识别、故障预测与诊断领域. KPCA 的思想是加入一个非线性函数Φ(x), 将样本数据映射到高维的特征空间F 中, 然后在F 中使用 PCA 方法进行降维. 因KPCA方法在数据存在异常点(outlier)时很敏感, 学者们对改进和提高KPCA的鲁棒性和稀疏性方面做了很多工作, 其中Kim(2020) [49]提出了一个基于1L 范数的 KPCA 学习算法并且进行了收敛性分析. 使用1L 范数来度量方差可以缓解传统学习算法使用2L 范数存在异常点时的较大影响, 新方法通过一个几何上可解释的等价形式证明了局部收敛性, 具有线性收敛速度, 缺点在于1L 范数是非凸非光滑的.
...............................
2 一种双目的 PCA 与 MCA 算法 DDT 系统收敛性分析
2.1 引言
PCA/MCA算法通常被刻画为随机离散时间(SDT)系统, 直接分析其收敛性是一项非常困难的工作. 为了克服这一不足, 通常根据随机逼近理论, 将随机离散时间(SDT)系统转换为与之相对应的确定连续时间(DCT)系统[ 63 ]. 这样就可以间接地分析PCA/MCA学习算法的收敛性能. 但采用DCT方法需要满足一些苛刻的限制条件, 其中之一便是要求2( ) 0, ( ) , ( ( ))k kηk > ηk = ∞ ηk < ∞ , 即当k→ ∞ 时,有 η(k) →0 . 但是在许多实际应用中, 学习率通常被设置为一个正的常数. DCT方法的这一缺陷大大地限制了它的应用.
Zufiria于2002年提出了一种确定性离散时间(DDT)系统[64]. 相比传统的DCT方法, DDT方法既保留了PCA/MCA学习算法的时间离散特征, 同时不要求算法的学习率必须趋近于零, 是一种更有实用价值的分析方法.
迄今, 尽管人们提出了大量的PCA/MCA学习算法, 但只有少量的论文通过DDT系统分析了这些算法并给出了确保算法收敛的条件[65-68], 而且其中大部分给出的只是算法收敛的充分条件, 只有非常少的论文给出了算法收敛的充分必要条件. 显然后者对算法的研究更为透彻、更加深入, 理论意义和实用价值也更大. 例如, 文[66]和文[67]分别对归一化PAST算法和改进的Oja-Xu MCA进行了研究, 得到了使算法收敛的充要条件. 这两篇论文的共同思想是在各自的原算法中增加了一个归一化步骤, 其优点在于使算法收敛, 并提高算法的数值稳定性, 而不足之处是使算法的计算复杂度有所增加.
本文基于 DDT 系统对所提出的一个双目的神经网络算法进行了收敛性分析, 给出并严谨地证明了确保该算法收敛的充分必要条件, 并通过仿真实验与已有的算法(包括双目的算法以及其他类型的算法)进行了对比, 仿真结果显示, 所提出的算法具有很好的收敛性能.
...................................
2.2 数值实验
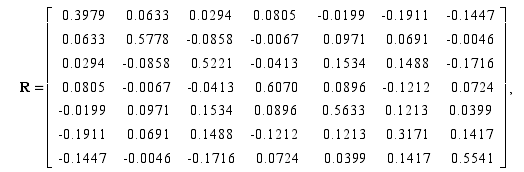
在这一节中, 我们做一些数值实验来验证算法1和算法2的收敛性能. 实验中我们使用如下7*7对称正定矩阵[69]
数学论文怎么写
3 PCA 和 MCA 神经网络学习算法的改进................................... 33
3.1 加入动量项的 PCA 和 MCA 神经网络学习算法......................... 33
3.1.1 归一化的投影近似子空间跟踪算法及其收敛性.............................. 33
3.1.2 带动量项的归一化投影近似子空间跟踪算法.................................. 36
4 基于宽度学习系统的股票价格预测........................................... 44
4.1 宽度学习系统......................................... 44
4.1.1 宽度学习系统概述......................................... 44
4.1.2 宽度学习系统的工作原理......................................... 45
结论 ......................... 53
4 基于宽度学习系统的股票价格预测
4.1 宽度学习系统
4.1.1 宽度学习系统概述
宽度学习系统(Broad Learning System, BLS)是由陈俊龙等学者于 2018 年提出的[72],区别于深度学习模型, BLS 是一种“平展型”的网络. 由于没有多层连接, BLS 不使用传统的梯度下降法更新权值, 因此其计算速度要优于深度学习网络. 在网络的学习精度达不到要求时, 可通过添加增强节点, 即增加网络的“宽度”来提升算法的精度. 相比深度学习模型增加层数, BLS 增加宽度所需增加的计算量要少很多. 宽度网络源于随机向量函数连接的神经网络(Random vector functional link neural network, RVFLNN). BLS 对RVFLNN 输入层进行了改进, 即不直接用原始数据作输入层, 而是先对输入数据向量做一些变换, 将提取后的特征作为原 RVFLNN 的输入层, 方便与其他机器学习算法混合. BLS 网络结构化简后(见图 4.1), 原来的输入层改称特征层. 对特征层与增强层之间的连接随机赋初始权值后, 从此便不再改变. 当给定了特征 Z, 可直接计算出增强层 H. 增强层单元上带有非线性激活函数, 而网络的其他部分均是线性的. 将特征层和增强层合并成一行得 A=[Z | H]. 因训练数据的理想输出 Y 已知, 通过伪逆即可计算出权重 W.

数学论文参考
..............................
结论
PCA/MCA 学习算法可以从高维输入向量样本中自适应地在线提取最大和最小主元, 应用广泛. 双目的 PCA/MCA 算法仅改变权值向量增量的符号即可实现对主、次元提取的转换, 这有利于减小计算的复杂度并降低硬件资源的开销. 尽管目前 PCA/MCA 研究领域取得了丰硕的成果, 但在算法及算法的性能分析方面仍存在着一些问题急待解决. 例如算法的收敛性分析、算法的收敛速度提升以及 PCA 和 MCA 两种算法之间有何内在联系等等. 本论文的主要工作概括如下:
(1) 基于确定离散时间(DDT)系统分析了一种双目的 PCA/MCA 学习算法, 提出并证明了一个确保算法收敛的充分必要条件. 与现有算法进行比较, 发现该算法具有形式简单、收敛速度快等优点.
(2) 将深度学习中用于提高网络计算效率、优化网络结构的经典方法——动量项和惩罚项技术引入到 PCA/MCA 学习算法的权值更新公式之中, 提高了算法的收敛速度和学习精度, 克服了算法迭代过程中出现的振荡现象.
(3) 使用带动量项的 GHA 算法与宽度学习系统(BLS)的混合模型对股票价格进行了预测, 取得了较为理想的预测结果.
参考文献(略)
