第一章 绪论
1.1 课题背景及研究意义
人工智能研究中一项重要的任务就是对不确定知识的表示和使用的研究。概率论和数理统计是国内外研究人员在早期研究过程中较为常用的工具。近年来随着贝叶斯理论的发展,使用贝叶斯理论解决不确定性问题逐渐流行[1]。自 20 世纪 50 年代中期开始许多研究者开始逐步对人类智能进行研究,并构建模型将其转化为系统。然而不确定性严重的阻碍了人工智能系统的快速发展。造成不确定性的原因有很多,且一般来说难以避免[2]。为了减少不确定性的影响,研究人员提出了许多高效的方法以解决不确定性问题。1970 年代,专家系统[3]在早期人工智能发展于研究中占据了重要地位。专家系统指将某一领域的专家知识以及业务人员通过实践积累的经验进行建模转换为行为系统,使人们能够通过构建的模型使用专家经验解决现实问题[4]。贝叶斯理论始于贝叶斯的论文[5],改变了研究人员未充分使用概率统计相关知识解决不确定问题的情况,让更多的研究者了解了贝叶斯网络的优势及其数理基础。自 1986 年开始,Pearl 在前人工作的基础上对先验概率进行了大量研究并提出了贝叶斯网络(Bayesian network,BN)。BN 的提出可以使研究人员更直观通过结构和参数了解各变量间的关系,降低了推理难度的同时更方便用户理解和学习。BN 自提出以来就与有着机器学习密不可分的联系,如机器学习中的分类问题。针对不同的分类问题,研究人员提出了朴素贝叶斯(Naive Bayesian,NB)、TAN 分类器、多维贝叶斯分类器等各类基于贝叶斯定理的分类方法。图 1-1 是 NB 和 TAN的结构示例图。

.图 1-1 NB(左) TAN 分类器(右)
1.2 国内外研究现状及发展动态
随着对 BN 研究的深入,BN 结构学习方法也与时俱进。BN 在 80 年代主要用于专家系统知识构建,而后逐渐转变为使用较少的先验知识,直至如今只从数据集出发进行BN 结构学习。当变量数量及数据量迅速增加时,变量间的关系变得更加错综复杂,通过专家知识构造 BN 较为困难且花费较高[10],而从数据中学习一个完全准确的 BN 结构又是一个 NP 难问题[11]。因此怎样直接通过数据集准确的构造 BN,是现阶段一个主要的研究目标,近来人们提出了许多方法以解决 BN 结构学习问题,本节将主要介绍 BN结构学习算法相关研究现状。
1.2.1 BN 结构学习算法研究现状
BN 结构学习问题可以理解为从数据中学习网络的拓扑结构。一般来说从数据中自动学习 BN 的结构有三种常用的方法,分别是基于约束的方法、基于评分搜索的方法和混合方法[2]。
基于约束的方法将 BN 结构视为变量间条件独立性关系的表示,因此通过条件独立性测试(Conditional independence,CI)检测识别变量之间的条件独立性关系及相关性关系。常用的统计学方法有皮尔森卡方检验[12]、互信息检验[13]等。基于约束的方法也是BN 结构学习的第一种被提出方法。典型的基于约束的算法如 Spirtes 提出的 PC 算法[14],以及更复杂的如 GS 算法[15]等。通常来说,首先通过假设检验用于从数据集中找到条件独立性,通过条件独立性集合得到 BN 结构。一旦学习了结构,就从数据集学习需要完全指定 BN 模型的条件概率分布。基于约束的 BN 结构学习算法运行时间一般来说是三类算法中最短的,但其构造的结果对 CI 测试的准确率依赖较高。当 CI 测试的集合过大时,集合中可能含有冗余节点,这可能导致 CI 测试准确率降低,同时当样本数据量不足时,也会导致高阶 CI 测试的可靠性不足,会导致结构准确率较低。
...........................
第二章 相关知识简介
2.1 BN相关知识概述
2.1.1 概率论基本知识
概率作为不确定性表达方法的重要工具之一,是 BN 结构学习及 BN 推理预测的重要理论基础。本节中将针对 BN 结构学习算法中涉及到的一些概率论基础知识,做出相应阐述。
由于 BN 分为结构与参数,因此一般来说构建 BN 分为两部分:结构学习和参数学习。本文主要关注结构学习相关工作。对于结构学习问题来说,一般情况下可以通过学习得到 BN 的等价类。
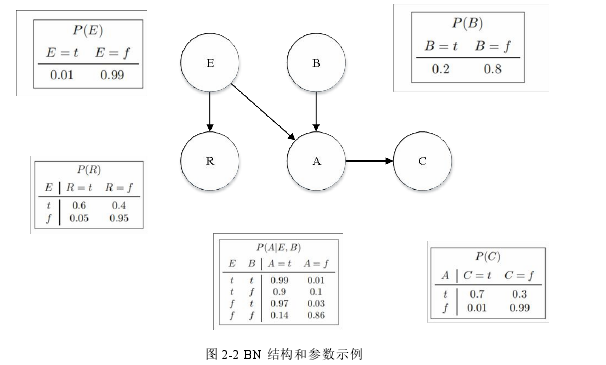
图 2-2 BN 结构和参数示例
2.2 BN结构学习算法概述
BN 结构学习问题是 BN 学习的核心之一,算法的目标是学习网络的拓扑结构。由于专家可以手动提供 BN 的结构,但精度无法保证,也很耗时,因此通过数据集自动学习 BN 结构是一项重要任务。通过数据集构造 BN 结构是一个 NP 难问题[11],学习大型复杂 BN 结构的任务难度更高,这种情况下得到一个结构完全准确的 BN 几乎是不可能的。近年来,许多研究人员开始关注 BN 结构学习,提出的解决方案也越来越多。一般来说,BN 结构学习算法可以被分为三类:基于约束(Constraint-based,CB)的方法、基于评分搜索(Score and search,S&S)的方法和混合方法。
2.2.1 基于评分搜索的方法
从基于评分搜索的方法的角度来看,BN 结构学习问题被理解为一个复杂的组合优化问题,基本思想是从可行的搜索空间中搜索到评分函数最高的 BN 结构。BN 结构评分较高代表此 BN 更拟合样本数据集。一般评分搜索方法分为两步:定义评分函数、采用搜索策略。评分函数对基于评分搜索学习 BN 结构来说十分重要,典型的评分函数有AIC 评分、BIC 评分、MDL 评分、BD 评分、BDeu 评分等。
BIC 评分由两部分组成,BN 结构的对数似然度和惩罚项函数。前者用来度量数据集与 BN 结构的拟合程度,后者用于避免由于结构模型过于复杂,参数过多,从而导致数据和结构过拟合的问题。
结构搜索方法的目的是在搜索空间中寻找到得分最高的 BN 网络结构,评分最高的BN 结构就是从样本数据集中所能学习到的和数据集拟合度最高的 BN 结构。典型的搜索方法如 K2 算法、HC 算法[20]等。K2 算法对节点排序进行搜索,HC 算法在搜索过程中每一次迭代中对差别较小的结构进行全量搜索,逐步对结构进行调整,得到评分更高的 BN 结构。对于每一次迭代,首先对当前的 BN 结构进行局部更新,更新后产生新的候选结构集合,作为当前步骤的搜索空间。而传统的单解搜索算法可能会陷入局部最优。由于寻找最优的结构问题是 NP 难问题,因此实际应用中常通过多次运行爬山法或使用启发式方法进行搜索。因此本文主要基于 GA 解决 BN 结构学习问题,GA 具体相关知识将在 2.3 节中进行介绍。
...................................
第三章 基于高效的知识驱动 GA 的 BN 结构学习算法................................ 22
3.1 引言...............................................22
3.2基于 GA 的 BN 结构学习算法.........................................22
3.3 EKGA-BN 算法..................................... 23
第四章 基于 Spark 和 GA 的分布式 BN 结构学习算法.............................33
4.1 引言.....................................33
4.2 分布式 BN 结构学习算法简介................................... 33
4.3 基于 Spark 和 GA 的 BN 结构学习算法设计................................34
第五章 结论与展望..............................54
5.1 结论................................54
5.2 展望......................................54
第四章 基于Spark和GA的分布式BN结构学习算法
4.1 引言
尽管很多学者在基于 GA 的 BN 结构学习算法的研究上已经取得了较多的成果,但大多数所提出算法的数据存储和计算模式仅针对单台计算机,内存和处理器的限制较大影响了能够使用的样本数据集规模和算法性能。虽然 GA 已被研究人员广泛的用于解决BN 结构学习问题,然而基于 GA 的 BN 结构学习仍是一个耗时的过程。基于分布式计算方法可以较好的摆脱单机算法的局限性,能够更高效的处理更大的数据集,同时减少算法执行时间以便更快的学习 BN 结构。基于 GA 的 BN 结构学习算法相比于许多单解搜索方法能学习到准确率更高的 BN 结构,因此我们将 GA 与基于分布式的 BN 结构学习算法进行了结合。由于 Spark 平台在基于迭代的计算过程和内存计算上优势较为明显,同时可以避免无意义的磁盘读写消耗及冗余的资源申请过程,相比 MapReduce 更适应基于 GA 的计算流程。因此为应对海量数据带来的繁重的计算挑战,本文使用分布式计算平台 Spark 以解决 BN 结构学习问题,提出了一种基于 Spark 的全流程分布式 GA 混合算法以便加速学习 BN 结构,称为 DGA-BN。提出的算法主要包括 SS 构造并行化、评分计算并行化和遗传操作并行化,首先通过 Spark 计算互信息构建 SS,同时保存相关中间过程计算数据,然后通过基于 Spark 的分布式 GA 算法进行搜索,减少了选择交叉算子的通信及落盘时间,并在每次迭代统一进行分布式评分计算,使用构建 SS 过程中数据的同时减少冗余计算,加快计算速度。在海量数据的情况下,在多个数据集不同数据量的数据集上进行了实验。
............................
第五章 结论与展望
5.1 结论
BN 结构准确率与预测准确率直接相关,而如何在有限时间内通过数据集自动构造准确率较高的 BN 结构是一直以来困扰着研究者,近来也涌现了许多相关的研究。在数据量不大的情况下,传统结构学习方法获得的 BN 结构准确率不高,而基于 GA 的算法又存在收敛速度较慢、易陷入局部最优的问题。海量数据情况下,现有的分布式结构学习方法又存在准确率不高,冗余计算较多的问题。因此本文对基于 GA 的 BN 结构学习算法进行研究,并提出了两种基于 GA 的 BN 结构学习算法:EKGA-BN 和 DGA-BN。在小数据量情况下提高了收敛速度与结构准确率,同时将基于 GA 的 BN 结构学习算法扩展到了海量数据情况下,加快了执行效率与准确率。
本文提出的EKGA-BN算法将爬山法的思想引入选择算子并通过知识驱动搜索过程改进变异算子,通过改进的遗传算法高效解决 BN 结构学习问题。首先定义了一个相同个体的最大数量,以保持种群的多样性。较高的种群多样性使得 EKGA-BN 结构更容易超越局部最优,因此学习得到的 BN 结构具有更好的性能。然后引入 HC 算法的思想,加快搜索每个小生境,从而加快收敛速度。此外,还分析了由表现良好的个体组成的精英集,以构建一个共同的 BN 结构。利用常用的 BN 结构来引导搜索方向,提高局部搜索能力。实验结果表明,提出的 EKGA-BN 算法相比单解搜索算法和基于约束的算法能够构建具有较高 BDeu 评分的较优的网络,并且在四个数据集上具有更快的收敛速度。EKGA-BN 在具有较多变量的数据集中也显示了相比更稳健且更显著的结果。
本文提出了一种使用 Spark 的并行混合算法,称为 DGA-BN,用于在海量数据情况下学习 BN 结构。混合算法的流程与 GA 并行化模型,DGA-BN 提供了全流程的并行化工作,全部工作分三个阶段。第一阶段是对构造 SS 的并行化,以便高效生成 SS。 第二阶段是遗传操作并行化,将各算子进行改造使各算子适应并行化操作并减少不必要的落盘次数加快效率。第三阶段使对 BIC 评分计算的并行化,同时引入 Redis,加大第一阶段和评分计算阶段中间计算数据的复用性减少冗余计算。据我们所知,DGA-BN 是使用 Spark 来并行化 GA 以学习 BN 结构的第一次尝试。通过对提出的多个并行方法通过消融实验的方式验证的有效性。相比串行 GA 算法,提出的 DGA-BN 方法在 BN 质量和算法效率上均有较好的表现,同时较好的扩展性。综上所述,DGA-BN 是 GA 在 BN 结构学习算法方面的一种有前景的改进。
参考文献(略)
