第 1 章 绪论
1.1 课题背景
2019 年是中国航天的“超级年”,这一年嫦娥四号登录月球背面,火星探测器亮相,中国的航天获得了瞩目的成就。无论是太空舱还是人造卫星都涉及仪器仪表的三维装填问题,对于加快建设中国航天强国也是至关重要的。卫星舱装填问题是本文研究内容,它不仅是一个耦合系统设计的问题,也是一个优化问题,具有 NPC 难度。
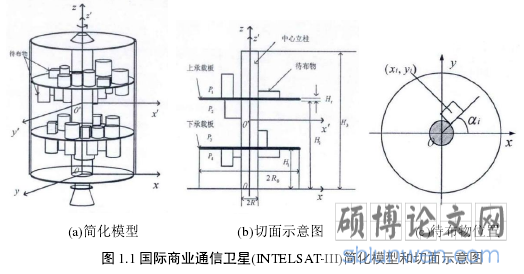
布局问题从布局区域的维度可以分为一维布局问题[4],二维布局问题[5],三维装填问题[6],二维布局问题按待布局的图形可以分为圆或矩形或多边形的布局问题,以布局的平面利用率为优化目标,例如钢材板坯的切割排版[7,8]、布料剪裁下料[9]、集成电路板的布线[10-12]。三维装填问题又将图形分为圆柱体立方体甚至是多面体的装填问题,以装填的空间利用率为优化目标,例如土木工程、集装箱装填、管道布局设计。布局系统有无性能约束例如稳定性,平衡性又分为带性能约束的布局问题和不带性能约束的问题。本文研究的卫星舱布局问题是性带能约束的装填问题,主要研究多舱卫星为简化的国际商业通信卫星(INTELSAT-III),如图 1.1(a)它要求将一定数量的圆柱体和长方体无重叠的放置在卫星舱的四个承载面上,使得卫星舱系统的转动惯量和包络半径尽可能小,同时满足质心偏移量和惯量夹角在约束的范围内并尽可能小。近几年的方法基本可以分为两类一是通过载荷质心在空间随机初始化并随机搜索,为载荷分配最优的装填位置;第二类是将问题转换为启发式序列优化问题,利用启发式方法定位和优化算法定序列。
........................
1.2 研究内容与意义
本文研究内容为两个部分。第一个部分对于不倒翁原理和转动惯量的研究,将获取的知识用于构建初始种群,加速算法的收敛和提高搜索能力,接着通过改进的启发式随机密钥遗传算法结合区域定位对负载配置和单舱装填进行协同优化,为载荷分配最优的布局方案解来降低转动惯量和包络半径。探索物理力学的知识,通过改进的粒子群算法来搜索承载面旋转的最优角度来进一步降低惯量夹角和质心偏移量。第二个部分对于平衡力学的研究,用获取的知识构建初始种群。接着对带有固定载荷的多舱卫星模型进行改进区域定位策略,启发式紧凑移动策略使得卫星舱整体的不平衡力、不平衡力偶和包络半径得到进一步优化,并提高了计算效率。
意义:本文研究的问题为卫星舱载荷的多舱装填问题,航空航天任务中要求将特定的仪器仪表放置在卫星舱内输送至太空中,而仪器仪表的放置位置和方向对于卫星的性能至关重要,它能影响到卫星舱的各项整体性能指标。本文设计智能优化算法解决载荷的配置和装填问题,提高太空舱的空间利用率,保证卫星在太空中能稳定完成任务,进一步提高经济效益和社会价值。
..................................
第 2 章 配置装填启发式随机密钥遗传方法
2.1 引言
卫星舱装填问题,载荷的配置方案对于卫星舱系统的整体性能具有较大的影响,求解出一个较优的配置方案至关重要。载荷的配置方案有人工初定[32]或启发式[18],但是到目前这些配置方案效果不佳。文献[1]尝试了演化过程进行舱间迁移的机制,但是在实数空间进行搜索同时还要进行舱间迁移较为艰难。同样基于随机初始点的演化算法[41,45-47]搜索空间巨大,并需要不断进行干涉判断耗时量大,本文提出了一种智能优化算法进行序列优化并与启发式布局相结合的机制,将搜索范围从复杂的实数空间转换为较简单的整数空间。文献[13,14,48,56]将装填方案分为负载配置和单舱装填两部分进行分部求解,通过第一部分求解出最优配置方案再在此基础上进行单舱装填,有效降低了搜索范围减少搜索时间,却因此丧失了部分优质解,使得整个算法容易陷入局部最优,于是对负载配置和单舱装填协同优化结合粒子群的多舱协同优化成为本文的求解思想,使得载荷能动态的舱内装填和舱间迁移,求解过程更具有灵活性,以提高求解精度。
..........................
2.2 卫星舱装填的数学建模
卫星舱装填问题属于带性能约束的布局问题,本章的研究背景是简化的国际商业通信卫星(INTELSAT-III),该问题的描述如下:将 N 个待布物(载荷)放置在如图 1.1 所示的卫星模型中,该卫星模型描述为:一个连接立柱上的两个承载板分成(P1-P4)四个承载面用于放置这 N 个待布物,设计的优化目标为卫星舱系统的转动惯量和整体包络半径尽可能小,约束条件为惯量夹角和质心偏移量在给定范围内并尽可能小。
........................
第 3 章 带固定载荷的多舱装填遗传方法.................................25
3.1 引言..............................25
3.2 问题数学模型.....................25
3.3 问题求解..........................26
第 4 章 总结与展望...........................33
4.1 本文总结..........................33
4.2 研究展望.................................34
第 3 章 带固定载荷的多舱装填遗传方法
3.1 引言
本章研究带固定载荷的卫星舱模型为返回式卫星回收舱,针对这种卫星舱的载荷装填目前存在的方法基于敏度分析[15]和启发式算法与演化算法[54-55,57-58]相结合,通过第二章我们了解到在载荷的配置方案的重要,但是到目前为止并不存在有效的配置方案。文献[58]方法分为配置和装填两阶段,通过知识进行载荷的配置,配置完毕之后载荷不能够再舱间迁移,后期装填时不能在算法的迭代过程中灵活的寻找最优的配置方案,本文提出了改进的随机密钥遗传算法用于载荷在迭代过程中能在装填的同时进行舱间迁移,扩大了解的搜索空间,同时采用了知识初始化种群减少了盲目搜索的所耗费的时间和空间,有效的优化了整体的性能并具备一定的稳定性;结合该模型带固定载荷的特性对区域定位进行改进并试探性的移动载荷,在较小影响包络半径这一指标下有效的降低动不平衡力偶和动不平衡力指标,进一步提高求解精度。目前的研究基本都是在较复杂的实数空间进行解的搜索[15,54,58],耗时量大,本文通过演化算法进行序列优化并与改进区域定位相结合来进行求解,将问题求解空间转换为较简单的整数空间,有效提高了求解效率。
...........................
第 4 章 总结与展望
4.1 本文总结
本文以多舱卫星载荷的装填问题为研究背景,基于平衡力学和惯性定义获取相关载荷配置与装填的知识,并受无免费午餐[46]定理启发与知识相结合提出了一种求解多舱卫星装填的启发式随机密钥遗传算法。基本思路仍是将问题进行降维求解、对目标问题进行分组求解,将问题转换为载荷的配置与装填的协同优化优化和卫星舱整体性能优化。本文存在四方面的优势:
(1)强大的搜索能力:在载荷的配置与装填阶段将知识个体引入算法的初始种群中,即其初始点很可能位于最小值点附近,因此能迅速找到高质量的解决方案,并为下一步的整体性能优化降低搜索时间。
(2)在低维整数空间中对装填序列的优化已取代了在高维实空间中寻找最优解,组合爆炸在某种程度上得到缓解。因此本文算法和 MSAPHAA[14]的计算效率均高于 CALO-DE[1]和 DVGCCGA[2]。但是对配置与装填阶段的协同优化,这点与 MSAPHAA 的分部优化不同,牺牲较小的搜索时间换取较大的搜索空间,实验结果表明本文算法求解精度和计算效率都具有优势。
(3)在载荷的单舱装填阶段能实现载荷的舱间迁移,比以往的算法都更具有灵活性进一步提高了算法的求解精度。
(4)与以往算法不同的,加入了半径的动态优化目标,并结合启发式式区域定位机制,能够在降低卫星舱载荷的包络半径的同时有效的降低转动惯量。
参考文献(略)
