本文是一篇计算机论文,本文首先给出子图匹配的研究背景与意义,同时论述了子图匹配在国内外的研究现状和ADD技术在图匹配领域的相关研究。然后给出了本研究所涉及的相关理论和基础知识。最后针对现有子图匹配求解算法存在的一些问题。
第一章 引言
1.1研究背景及意义
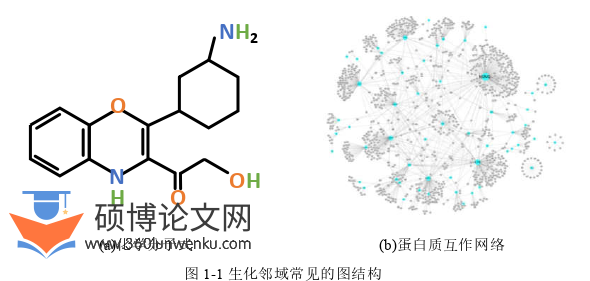
图作为一种重要的数据结构,可以有效刻画事物之间的关系,现实世界中的许多复杂问题都可以使用图进行抽象表示,在社交网络[1]、蛋白质互作网络[2]、化学[3]、交通运输网络[4]等领域广泛应用。在图中事物用节点表示,相应两个事物间的关系则用连接两个节点的连边表示。如图1-1所示,在生化邻域中图结构普遍存在,在图1-1(a)中化学分子是天然的图结构,原子表示为节点,原子间的化学键表示为边,图1-1(b)中蛋白质互作网络图表示蛋白质之间的相互作用,其中蛋白质分子表示为一个节点,它们之间的相互作用关系表示为边。此外,交通运输网络由复杂的交通运输线路构成,其中节点代表分岔路口,而边则表示路口之间的交通道路[5],节点之间的距离可以作为标签附加到边上,通过图论的相关理论可以计算两个节点之间的最短距离,并且可以衡量运费与距离之间的关系,从而选择适合的交通运输道路。
计算机论文怎么写
综上所述,图可以直观描述许多现实世界的问题,并应用相关理论与方法进行解决。随着互联网飞速发展与普遍应用,数据的规模呈指数级增长,数据之间的联系也越来越复杂。据CNNIC统计,2021年网页数量为3350亿个,较2020年增长6.2%,网民规模达10.32亿[6]。此外,各大社交网络的用户数量激增,如微信统计全球每月有12.6亿活跃用户。由于数据规模的日益增长,图数据的高效查询与管理成为一大难题。其中,图数据查询的基础是确定图结构的相似性,这促使图匹配问题[7]引起了广泛的关注,并成为当前学术界的研究重点。
.............................
1.2国内外研究现状
1.2.1子图匹配研究现状分析
在学术与工业界,两个图之间的相似性衡量有着重要的作用,因此图匹配相关技术的研究受到了广泛的关注,是目前研究热点之一。图匹配根据相似程度分为非精确图匹配和精确图匹配。其中,非精确图匹配研究着重点在于如何在较短的时间内寻找一个近似解或者局部最优解,该方式通过牺牲匹配精度换取时间效率[21]。精确图匹配的则需要两个图的节点间存在一一映射关系,保证两个图的结构与属性完全相同。根据应用场景的不同,精确图匹配的研究可分为图同构、子图同构与最大公共子图。
本文的研究内容是针对子图同构问题,该问题为确定是否存在从一个给定图的节点到另一个图的子图节点保持一对一映射[22]。由于子图同构匹配问题属于NP难问题,在最坏的情况下,其求解需要指数级的时间与存储空间。为此,许多学者从不同的角度提出了大量的子图同构匹配算法。其中,许多算法最终求解采用回溯法搜索解空间树,基于回溯树搜索的算法是通过将查询图节点映射到数据图节点,从初始空状态迭代的加入新匹配节点对以扩展部分匹配结果,同时采用一些剪枝策略以尽可能早的修剪无效的搜索路径,在搜索过程中,若当前节点匹配对不满足匹配约束条件,则回溯至上一步重新选择匹配节点对,直到找到所有可行解。下面将对已有的子图同构匹配算法存在的主要问题、代表性方法、研究现状进行分析。
著名的Ullmann算法[23]于1979年提出,该算法基于回溯的树搜索在数据图g中枚举出与查询图q匹配的所有子图。由于Ullmann算法只采用了简单的剪枝策略并且未考虑节点匹配顺序,无法高效地减少搜索空间,其时间复杂度为O(n!n2),只能处理小规模的数据图。此后,有许多算法在Ullmann算法的基础上做出了改进。Cordella等人提出在状态空间表示(State Space Representation, SSR)中形成子图匹配,其中每个状态表示一个中间结果,并给出了VF[24]和VF2[25]算法,VF2算法使用一组可行性规则,将邻接节点的结构与语义信息作为约束条件增强了剪枝效果,显著地减少了搜索空间,且时间复杂度为O(n!n),有效地提升了匹配求解效率。
........................
第二章 相关理论介绍
2.1图匹配理论基础介绍
图是离散对象的直观抽象模型,通常将对象刻画为节点,对象之间的关系刻画为边,以此来描述现实世界中的许多问题,这样可以采用图论的相关理论对其进行研究解决。本文针对节点带有标签的标签图进行的子图匹配算法研究,图的相关定义如下:
定义2.1:图可表示为二元组G=<V, E>,其中V={v1, v2, …, vn}是节点集合,和E={e1, e2, …, en}是边集[54]。
定义2.2:在图G=<V, E>中,节点v∈V为端点出现的次数称为节点v的度数(degree),简称度,记为d(v)[54]。
定义2.3:在图G=<V, E>中,节点u到v的通路满足u=v,则称该通路为经过节点u的回路。
定义2.4:若节点vi与vj之间存在边连接,则称vi和vj互为邻接节点,vi的邻接节点的集合写为Nvi。如果vj到vi的距离为k,则称vj为vi的k阶邻接节点。
定义2.5:在图G=<V, E>中,若节点vi∈V表示一个节点,eij=(vi, vj)∈E表示vi与vj存在边连接,邻接矩阵表示节点之间的连接关系,其中n为图G中的节点数,如果ije ∈E,则ijΑ=1,反之ijΑ=0。节点特征矩阵n×dΧ∈¡表示节点的属性,其中dvx∈¡表示节点v的特征向量。
定义2.6:标签图G=<V, E, L, l>,其中V表示图G的节点集合,E表示图G中所有的边集,L表示节点标签集合,l表示标签映射函数:V→L。
图匹配问题是在两个图的节点和边之间找到对应关系,确保一个图中的子结构映射到另一个图中的相似子结构。本文主要是研究精确图匹配问题中的子图同构匹配问题,下面给出相关定义。
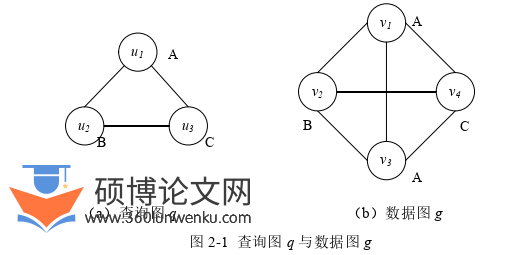
计算机论文怎么写
.....................
2.2图神经网络相关技术
图神经网络具有强大的学习表示能力,主要通过递归传播和聚合邻居信息得到目标节点特征向量,从而使得该向量包含了目标节点的邻域信息[55]。本文将采用图神经网络提取图的节点特征向量,主要基于图卷积神经网络(Graph Convolutional Network, GCN)和图注意力神经网络(Graph Attention Network, GAT)实现,下面详细介绍对GCN和GAT的原理和结构。
2.2.1图卷积神经网络
由于初期图神经网络[18]在训练过程中工作量庞大,研究学者受到卷积神经网络的启发将卷积操作从图像数据推广到图结构数据,从而提出了图卷积神经网络,其主要思想是聚合节点自身的特征xv和邻接节点特征x Nv生成节点v的特征表示。文献[19]给出了基本的GCN模型如图2-2所示,在图的卷积层中,每个节点的深层表示是通过邻接节点特征信息聚合得到,并在聚合邻接节点特征后进行非线性变换,然后叠加多层卷积层,使得每个节点的最终特征表示能够包含来自k阶邻接节点的信息。GCN依据特征空间大致可以分为两类:基于频谱域的卷积和基于空域的卷积。
基于频谱域的图卷积采取频谱分解的方式[56-58],通过图的拉普拉斯矩阵分解得到节点特征。该方法具有一定的理论基础,可以基于图信号滤波器设计新的图卷积网络。然而,基于谱域的模型有些难以克服的缺点,计算代价会随着图规模得增加而急剧增加,其特征分解计算复杂度为O(n3)并且空间复杂度为O(n2),这使得它们很难适用于大型图。
.............................
第三章 基于图神经网络的子图匹配符号算法 ........................ 18
3.1基于图神经网络特征提取的过滤技术 ........................ 18
3.1.1图神经网络模型 .............................. 18
3.1.2候选节点过滤方法 .................. 19
第四章 基于ADD的子图同构过滤算法 ...................... 33
4.1改进的候选集ADD表示 ................................... 34
4.2搜索过滤顺序设计 .............................. 34
4.3改进的搜索过滤策略 ....................... 35
第五章 总结与展望 ................................ 41
5.1主要研究工作总结 ..................... 41
5.2存在问题与展望 ........................... 42
第四章 基于ADD的子图同构过滤算法
4.1改进的候选集ADD表示
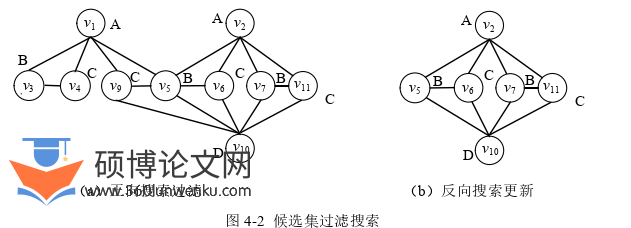
根据3.3.1节中提到的候选区的ADD表示,得知查询图每个节点的候选集在每个候选子区中的分布不同。在并行搜索时,这将导致不同候选子区中存在冗余候选节点,为此,需要依据候选区对节点候选集进行划分,使得可以并行剔除在不同的候选区中错误的候选节点。于是新的候选集ADD表示需要使用三组布尔变量分别表示查询图节点、候选区以及数据图节点。记为(Z, X, Y)=(z1, z2, …, zm, x1, x2, …, xm, y1, y2, …, ym)。其中Z变量表示候选子区的标志,X变量表示查询图节点,Y变量表示数据图节点。在给定变量序π:z0<z1<x0<x1<y0<y1的情况下,便可得到候选集的ADD表示。下面将通过图4-1举例说明。
已知候选区R1的候选集为:(u1,{v1}), (u3,{v4}), (u6,{v9}), (u2,{v3,v5}), (u4,{v3,v5}), (u5,{v8,v10})。由于数据图g的节点数量为11,故图中节点编码长度为4。在此,将采用节点下标的二进制串作为每个节点的编码,如查询图中节点u1,u2的编码分别为0001,0010。故u1在候选区R1的候选集的编码为000100010001,其对应的布尔变量表示为:'''''''''0 1 2 3 0 1 2 3 0 1 2 3z z z z x x x x y y y y,以此类推,可以得到其他节点的候选集编码以及布尔变量表示,由此可以得到R1区的候选集ADD表示。
计算机论文参考
..........................
第五章 总结与展望
5.1主要研究工作总结
子图匹配是实现图数据高效处理的重要方法和手段,被广泛应用于图像检索、化学分子式检索、知识图谱查询和社交网络分析等领域。本文致力于提高子图匹配算法的求解效率。由于图神经网络能够很好的提取图中节点的邻域结构与属性信息作为节点特征,并且ADD作为一种隐式存储结构,具有高紧凑性的特点,能够有效缓解传统算法中的状态组合爆炸问题。为此,本文引入图神经网络相关技术并结合ADD对子图匹配问题求解技术进行研究。本文首先给出子图匹配的研究背景与意义,同时论述了子图匹配在国内外的研究现状和ADD技术在图匹配领域的相关研究。然后给出了本研究所涉及的相关理论和基础知识。最后针对现有子图匹配求解算法存在的一些问题,本文对其做出了相应改进,主要工作包括:
(1)从改进过滤技术、优化匹配顺序和减少冗余搜索三个方面出发,提出了基于图神经网络的子图匹配符号算法SSMGNN。该算法采用图卷积神经网络聚合图中节点的邻接节点的结构和属性信息以得到节点的特征向量,并以该向量作为过滤条件,优化剪枝策略。其次,综合考虑节点候选集的大小、节点度数以及待匹配节点的邻居中已匹配节点数等信息,给出了一种新的优化匹配顺序。然后,引入了符号ADD存储结构,在数据图中实现各候选区域的并行运算与公共子图的共享存储。并在公开数据集上对该算法进行实验验证,与目前普遍认可的用于集中式查询处理的算法VF3相比,具有明显的优势。
(2)对SSMGNN算法作进一步改进。在提取节点特征信息时引入图注意力网络提取节点特征向量,聚焦节点间的关键信息,并借鉴节点重要性的计算方法对注意力系数提出了改进,改进后的算法称为SSMGAT。实验表明,采用新的特征提取方法能够更好地表示图中节点的局域信息,从而提高子图匹配求解效率。
参考文献(略)
