本文是一篇金融论文,本文从时频视角出发,基于Copula函数对股票市场中主板、创业板和新三板市场间的风险溢出效应进行研究,并对基于主板、创业板和新三板市场的投资组合风险进行时频测度。
第一章 绪论
1.1研究背景和意义
2003年,国务院首次提出要建立多层次资本市场体系的决议。2009年,创业板的推出意味着我国多层次资本市场体系建设更进一步。2013年初,全国中小企业股份转让系统正式挂牌,新三板设立,这一举措进一步完善了我国多层次资本市场体系的组成部分。随着我国股票市场的不断发展,目前已形成由主板、创业板、新三板和区域性股权交易市场构成的多层次资本市场体系。在当今全球金融化的大环境下,我国股票市场体系不断完善与发展,使得市场间的联系越发紧密,各类资源流动更加迅速,信息的传递效率也得到了很大提高。但是,在这种情形下,随着市场关联性的不断加强,一旦某个市场出现经济波动,并引发金融风险,则会很快蔓延进而影响另一个市场。而且目前股市不完善的运行机制与投资者不成熟的投机行为,都会加剧这种市场波动,进而促进波动的蔓延,引发股市不同板块间的风险溢出。为了监测金融市场风险并建立有效的风险预警机制,研究股市不同板块之间的风险溢出效应是有帮助的。本研究可以为监管机构提供实证依据,以便监管机构能够加强对主板、创业板和新三板三个市场板块的联合监管,从而维护金融市场的稳定。
值得一提的是,在当前供给侧结构性改革大背景下,党的十九大报告提出要“健全金融监管体系,守住不发生系统性金融风险的底线”,这对于当前经济发展至关重要。并且中国货币政策执行报告及中国金融稳定报告亦曾多次提及要防控金融风险。正如习总书记所说,当前金融工作的永恒主题就是防范化解系统性金融风险。而股票市场作为我国金融市场极为重要的组成部分,在此背景下,对股市不同板块间的风险溢出进行研究,契合当前国情。与此同时,目前研究多基于原始时间序列,即基于时域的考量,缺少频域视角。而实际上,不同的投资者具有不同的投资周期偏好,进而在不同的交易周期上进行交易。因而,在研究股票市场不同板块间的风险溢出过程中,有必要立足于时频双域视角进行研究。为此本文在时域与频域综合考量的多级尺度下,考察我国股票市场不同板块间的风险溢出效应,并对相应市场的投资组合进行风险测度,具有重要的理论与学术价值,同时亦具有重要的实践指导意义,有助于更好地理解股票市场不同板块之间的风险传导机制,并提供相应市场的投资组合风险测量模型和方法,有利于投资者优化投资决策与加强自身风险控制,减少投资过程中的盲目决策行为,为股票市场体系的风险防范和健康发展提供可供参考的模型与方法。
................................
1.2国内外研究现状
1.2.1股市不同板块间的风险溢出研究
首先,对于主板和创业板间的风险溢出研究,王旻等(2009)对香港股市主板与创业板市场在波动性与流动性方面进行研究,发现存在主板向创业板的单向溢出。张金林和贺根庆(2012)对创业板市场和沪深主板市场之间的动态联动性和波动溢出进行研究,发现这两个市场间的波动性是时变的,且就波动强烈程度而言,创业板明显高于主板。曾志坚等(2012)借助小波分解方法对创业板与主板市场间的风险溢出进行了相关研究,发现在交易周期较短时,溢出效应不存在;而随着交易周期的延长,两者间的均值溢出效应会从无到单向再到双向逐渐显现,而波动溢出效应则没有规律性。谢家泉和许均平(2013)借助GARCH-Diagonal-BEKK模型研究了创业板与主板市场间的溢出效应,发现主板到创业板存在均值溢出;而创业板与主板间也有双向波动溢出,两个市场的波动相关性随着创业板的发展而逐步提升。邹海荣等(2014)实证分析了创业板和主板间的溢出效应,发现这两个板块间的溢出强度并不一致,创业板对主板市场的波动溢出强度更大。李立林和施建业(2021)使用BEKK-GARCH模型对沪市主板和深市创业板间的溢出效应进行研究,发现它们之间存在显著的双向溢出。
其次,对于主板和新三板间的风险溢出研究,黄艳芳(2016)通过BEKK-MVGARCH模型对新三板市场与沪深主板市场间的风险溢出效应进行研究,发现溢出方向主要为主板对新三板市场的单向溢出,且新三板对主板的下跌产生的冲击相较于上行冲击反映更为强烈。欧阳颖等(2017)研究了新三板与沪市主板及深市主板间的溢出效应,发现深市主板对新三板存在较为显著的单向溢出,而新三板市场对沪市主板和深市主板均不存在显著溢出效应。何金曙(2017)通过VAR模型对新三板市场和主板市场间的均值溢出效应进行了研究,发现新三板与主板市场间存在显著双向均值溢出。
.............................
第二章 相关研究基础
2.1小波变换基础
2.1.1离散小波变换
离散小波变换(Discrete Wavelet Transform,DWT)是小波分析的一种形式,在金融领域中被广泛应用,特别是在金融时间序列分析中。通过DWT,可以将金融时间序列分解为一系列不同频率的分量,从而可以对金融时间序列的长期趋势、短期波动等特征进行更加准确的分析和预测(Donald和Andrew,2006)。
2.1.2极大重叠离散小波变换
极大重叠离散小波变换(MODWT)能将一个序列转换为与一组尺度上的变化相关的系数。相较于DWT,MODWT更灵活,可以通过可变窗口信号的时间频率来表示。此外,MODWT能够处理任何长度的时间序列,因为它在每个尺度上都是完全重叠的,并且可以使用不同长度的小波滤波器来适应不同长度的数据。这种优势避免了DWT对时间序列长度为2的幂次的限制,使得MODWT更加通用。与DWT不同,MODWT因为其低冗余和非正交性,减少时间序列起点选择对结果的影响。在分解过程中,它会生成一系列的小波系数,包括逼近系数和细节系数,这些系数提供了更多的信息以帮助分析数据。此外,MODWT能够将含有综合信息的信号分解为单一特征信号,从而更精确地了解信号的特征和结构,避免被无关的细节所干扰。因此,MODWT在信息提取方面更加完整和全面。
...................................
2.2 Copula函数

金融论文怎么写
Copula函数是一种统计工具,用于描述不同变量之间的依赖关系。在金融风险管理领域,Copula函数被广泛应用于研究金融风险溢出。金融风险溢出是指一个市场的波动对其他市场的影响,通常是由于不同市场之间的关联性。Copula函数具有很多优势,可以帮助研究者更好地理解和量化不同市场之间的关联性,从而更准确地评估风险溢出。
首先,Copula函数可以独立地描述不同市场之间的关联性和各个市场的边际分布。这意味着研究者可以将不同市场之间的关系和各个市场的风险特征分开考虑,从而更好地理解市场之间的关系。这对于评估风险溢出非常重要,因为不同市场之间的关系可能非常复杂。Copula函数的独立性使得研究者能够更好地理解市场之间的关系,从而更准确地评估风险溢出。其次,Copula函数可以通过构建多维联合分布来模拟不同市场之间的关系。这使得研究者能够更好地理解市场之间的交互作用,并预测风险溢出的可能性。最后,Copula函数可以用于构建金融风险管理工具,如投资组合的VaR。通过使用Copula函数,可以更准确地计算投资组合的风险,从而更好地控制风险。参考韦艳华和张世英(2008)的研究,下面对本文所使用到的Copula函数进行阐述。
.....................................
第三章 时频视角下基于Copula函数的股市板块间风险溢出效应研究 .................... 25
3.1 数据选取与处理 .............................. 25
3.2 基于MODWT的收益率序列多尺度分解 ...................... 25
3.3 基于Granger因果检验的风险溢出方向分析 ............................. 29
第四章 时频视角下基于Copula函数的股市板块间投资组合风险测度研究 ................................ 57
4.1 基于Copula函数的股市板块间投资组合风险静态测度 ........... 57
4.1.1 基于二元Copula函数的投资组合风险静态测度 ................. 57
4.1.2 基于多元Copula函数的投资组合风险静态测度 ................. 60
第五章 结论与政策建议 ...................... 73
5.1 研究结论 .............................. 73
5.2 政策建议 ........................ 75
第四章 时频视角下基于Copula函数的股市板块间投资组合风险测度研究
4.1 基于Copula函数的股市板块间投资组合风险静态测度
4.1.1 基于二元Copula函数的投资组合风险静态测度
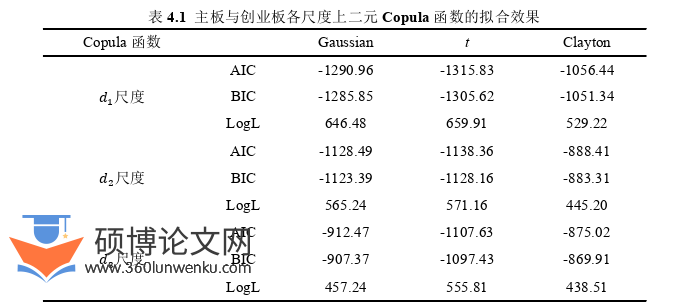
本节使用了三种常见的二元静态Copula函数,分别是Guassian-Copula函数、t-Copula函数和Clayton-Copula函数对概率积分变换后的主板与创业板、主板与新三板以及创业板与新三板间的收益率序列进行拟合,参考黄晓凤,王廷惠和程玉仙(2015)的研究,本节依旧是按照最大似然值LogL 、最小AIC和BIC的原则进行最优二元Copula函数的选取,具体每种Copula函数的拟合情况如表4.1、表4.2和表4.3所示。
根据表4.1、表4.2和表4.3在各尺度下基于不同二元Copula函数拟合结果可以看出:(1)在各尺度上,对于沪深300指数收益率序列与创业板指收益率序列,二元t-Copula函数的拟合效果最优,其AIC和BIC的值均最小,且LogL 均最大;(2)在各尺度上,对沪深300指数收益率序列和三板成指收益率序列来说,依旧是t-Copula模型对它们的相关关系拟合效果最优,其AIC和BIC最小,LogL 最大。(3)对创业板指和三板成指收益率序列而言,在� 尺度上Gaussian-Copula函数的AIC和BIC最小,在其他两个尺度上,均是t-Copula的AIC和BIC最小 且LogL 最大,因此t-Copula依旧是拟合创业板和新三板的最优Copula函数。因此,综合各板块收益率序列在各尺度上的拟合效果,本节选用t-Copula作为拟合两两板块间的最优Copula函数。
金融论文参考
..............................
第五章 结论与政策建议
5.1 研究结论
针对现有研究存在的不足及可改进的地方,本文基于时频视角和动态视角,研究同时考虑三个市场综合作用下的风险溢出效应,并测度了投资组合的时频风险,对现有研究进行了扩展。首先,基于MODWT方法对股市三个板块原始收益率序列进行分解,并使用格兰杰因果检验以判定板块间在各尺度上的溢出方向;其次,使用动态Copula函数对概率积分变换后的各尺度序列进行拟合,并计算出动态CoV a R等风险溢出强度指标以判定各板块在不同尺度上的风险溢出强度大小;最后,在时频视角下基于Copula对股市板块间的投资组合进行风险时频测度,基于静态Copula函数使用蒙特卡罗模拟对投资组合在各尺度上的风险静态Va R进行测度,并基于动态Copula函数将蒙特卡罗模拟与滚动窗口法相结合对投资组合在各尺度上的风险动态VaR 进行测度,再基于二元和多元Copula函数,对投资组合的风险VaR 测度结果进行对比分析。根据本文的主要研究内容,具体得到如下结论:
(二)时频视角下基于Copula函数的股市板块间风险溢出效应研究
①在各尺度序列的Copula函数的拟合上,静态和动态t-Copula函数的拟合效果均最优。②从动态相关系数来看,在各尺度上,主板与创业板间的动态相关系数均值最大且标准差最小,说明两个板块间呈强正相关性且波动较为稳定。而主板与新三板、创业板与新三板间均呈弱正相关性且波动程度较高。随着尺度的增加,主板与创业板间的动态相关系数均值逐渐降低,标准差逐渐增大。③从动态CoV aR 、ΔCoV aR 和%CoV aR 等指标来看,在各尺度上,创业板对主板的溢出强度大于主板对创业板的溢出强度,主板对新三板、创业板对新三板的溢出强度均较大,随着尺度增加,板块间风险溢出强度逐渐减小。在较小的尺度下,市场中的一些短期投机因素会对风险溢出关系产生较大影响,但随着尺度的增加,这些短期因素会逐渐被平滑掉,市场也会逐渐恢复到长期平衡状态。④使用多元动态t-Copula模型相对于二元动态t-Copula模型更能准确地描述三个市场之间的联动关系,不同板块间不同尺度上均存在不同程度和方向的风险溢出效应,并且基于多元Copula同时考虑三个市场板块综合作用下所测度出的风险溢出强度相比于只考虑两个市场所测度出的风险溢出强度会更大。这是因为考虑多市场板块风险耦合的情况下,板块之间存在风险相互叠加作用,以及风险的扩散效应,因此测度出的板块间的风险溢出强度会更大。
参考文献(略)
