本文是一篇博士论文,本文主要基于互补型偏好信息的个体偏好信息一致性、群体共识性及残缺元素补全问题展开了深入探讨,采用以粒子群优化算法为代表的智能算法对所建立的模型进行求解。
第一章绪论
1.1研究背景及意义
当前,随着我国经济进入高质量发展阶段以及人工智能、大数据等信息技术的不断发展,众多企业在制定各种发展方案、确定各项决策时的复杂性和不确定性日益加强,使得做出一个科学、合理的决策面临着重重挑战。比如,在选择供应商时,企业需要考虑价格、质量、交货期、信誉和可靠性、技术支持以及合作兼容性等因素;在选择低碳行业进行投资时,企业需要综合考虑政策环境、市场需求、技术成熟度、资金成本、人才储备和产业链协同等因素;在选择购物中心地址时,企业需要综合考虑交通便利性、竞争环境、人流量以及商业配套设施等因素;在选择直播带货平台时,企业需要综合考虑目标受众、平台流量、费用与成本效益、稳定性与技术支持以及口碑与品牌形象等因素。由此可知,决策问题大量地客观存在于现实生活之中,需要我们积极面对和处理。因此,给出一个恰当的决策方法是十分必要的。目前,有关决策问题的研究日益成为现代科学的重要内容。
为了解决社会经济领域中的决策问题,美国著名运筹学家Saaty在20世纪70年代初期提出了层次分析法(Analytic Hierarchy Process,简称AHP)[1,2]。在AHP中,决策者需要把决策问题分解成一个多层次结构,包含目标层、准则层、方案层等。决策者通过对各准则之间和各方案之间进行两两比较,构造出多个互反型偏好信息(也称积型偏好关系、互反判断矩阵),并依据权重的确定方法分别给出准则的权重和方案的权重,然后进行综合得到最终的排序权重从而对各方案进行排序。AHP面对的是内部独立的低阶层次结构,而对于内部依存的网络结构,Saaty在1996年提出了适应这种复杂结构的决策科学方法——网络分析法(Analytic NetworkProcess,简称ANP)[3]。目前,以AHP和ANP为基础的决策理论和方法,吸引了国内外大量学者的关注和研究并将继续完善和发展[4,5]。
......................
1.2国内外研究现状
对于一个决策问题,决策者需要对一组方案进行两两比较并给出其偏好信息,最常用的有三种类型的偏好信息:互反型偏好信息[1]、互补型偏好信息[8,9]和语言型偏好信息[25]。群体决策的目标是协调决策者之间的意见,进而寻求群体广泛支持的方案。在共识达成过程中,为了做出科学合理的决策,需要考虑两个重要方面:(1)决策者提供的个体偏好是否具有满意一致性;(2)是否达到一定程度的共识水平。其中,个体偏好满意一致性是为了保证决策者提供的偏好信息是可信的,而达到一定程度的共识水平是为了保证群体偏好信息被大多数决策者接受。同时,若决策者提供的偏好信息出现残缺,应当采用合理的方式进行补全。本文主要关注基于互补型偏好信息的决策理论与方法。目前,国内外众多学者在互补型偏好信息的个体偏好信息一致性、群体共识和残缺偏好信息补全等方面做了大量的研究工作,具体如下:
1.2.1偏好信息一致性
互补型偏好信息的加型一致性主要是基于偏好信息之间的加法关系,关注的是偏好信息之间的相对差异是否保持一致。目前主要通过两个角度来量化互补型偏好信息加型不一致性程度[27-35]:一是基于加型一致性定义建立指标[27-30];二是基于加型一致性互补型偏好信息与原互补型偏好信息的偏差程度来建立指标[31-35]。此外,Liu等[36]根据互补型偏好信息两行或两列的关系,提出新的加型一致性指标并给出相应的阈值。同时,对于一个互补型偏好信息,若其加型一致性程度较低,通常用基于迭代或者优化的方法来进行调整[31-35,37]。从基于迭代的角度,杨静和邱菀华[31]从加型一致性定义推导出加型一致性指标并设计迭代算法对部分偏好信息进行修改来提高加型一致性。Wu和Xu[32]及Meng和Chen[33]分别给出了一个迭代算法对互补型偏好信息进行全局修正。Liu等[34]基于主客观调整系数设计了一个迭代算法使调整后的互补型偏好信息具有满意加型一致性。从基于优化的角度,Xu等[35]基于距离公式建立最优化模型来提高互补型偏好信息的加型一致性。
............................
第二章理论基础
2.1互补型偏好信息的相关知识
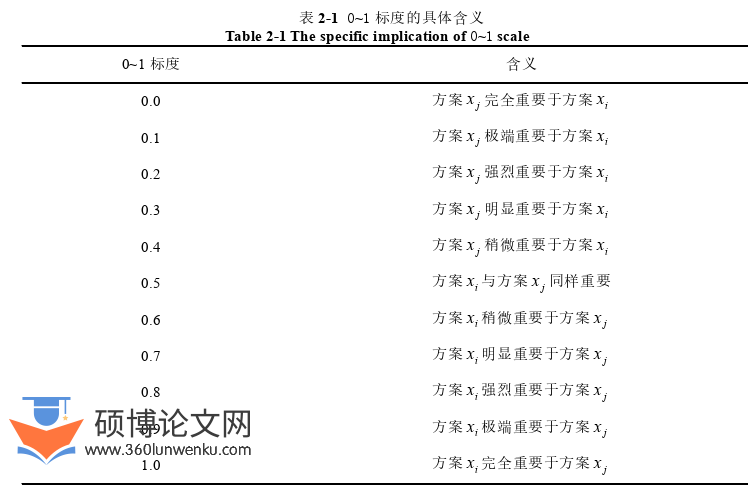
模糊层次分析法研究的核心问题是构造合理的偏好信息,在此基础上得到合理的方案排序。判断一个偏好信息是否合理,主要是通过偏好信息的一致性性质来检验。当决策者对备选方案进行成对比较并用区间[0,1]内的实数来表达方案之间的偏好强度时,得到的偏好信息就可以表示为互补型偏好信息。此外,随着计算机技术的发展,以粒子群优化算法为代表的智能算法为解决复杂环境下的决策问题提供了新的思路和方法。
博士论文怎么写
....................
2.2粒子群优化算法的相关知识
在自然界中,人们通过观察发现群居性生物如蚁群、鸟群等简单个体在特定任务或环境下,通过协作在解决问题上的表现超越绝大多数个体。如蚁群在觅食过程中,能够通过信息素的传递与协作,找到从巢穴到食物源的最短路径;鸟群在迁徙时,能够形成有序的队伍,减少空气阻力,提高迁徙效率。这些现象展示了群体的智慧在解决实际问题中的潜力。群居性生物通过内部协作表现出的宏观智能行为特征被称为群体智能。随着计算机技术的发展,人们开始尝试模拟这些自然现象,通过算法实现群体智能。
作为一种经典的群体智能算法,PSO算法因易于实现、收敛速度较快等优点,自提出以来受到广泛关注,已在很多复杂优化问题的求解当中取得了很好的效果[182-184]。下面介绍相关知识。
2.2.1初始粒子群优化算法
美国心理学家Kennedy与电气工程师Eberhart[185]通过模拟鸟群觅食行为,于1995年在IEEE国际神经网络学术会议上发表了题为“Particle Swarm Optimization”的文章,正式标志着PSO算法的诞生。PSO算法的核心思想是将优化问题的潜在解看成粒子,每个粒子需要在解的范围内进行运动,粒子需要在运动过程中不断调整速度和方向,其依据两方面:一是个体最优位置,即粒子迄今找到的最好位置;二是全局最优位置,即整个种群迄今找到的最好位置。
........................
第三章 基于偏好信息加型一致性优化控制的群体决策模型及其应用 ..................... 22
3.1 引言 ............................ 22
3.2 互补型偏好信息的序列模型 ............................. 22
第四章 基于偏好信息积型一致性优化控制的大规模群体决策模型及其应用 ............................... 38
4.1 引言 ...................................... 38
4.2 积型一致性修正模型 ...................... 38
第五章 基于偏好信息弱传递性优化控制的群体决策模型及其应用 67
5.1 引言 ....................... 67
5.2 弱传递性修正模型 .......................... 67
第六章基于残缺偏好信息序列分析的决策模型及其应用
6.2残缺互补型偏好信息的序列模型
在实际决策问题中,由于决策环境的不确定性等因素,决策者在0~1标度下对备选方案进行成对比较时可能无法给出偏好信息,此时最终得到的互补型偏好信息是残缺的,即残缺互补型偏好信息。以往的研究都是基于最终得到的残缺互补型偏好信息,没有考虑专家给出偏好信息的过程。类似于互补型偏好信息的序列模型,为了刻画决策者给出偏好信息的完整过程,本文考虑方案比较过程的序列性和复杂性,建立残缺互补型偏好信息的序列模型。
下面以残缺互补型偏好信息R1为例,进行说明:

博士论文参考
......................
第七章结论与展望
7.1研究结论
本文主要基于互补型偏好信息的个体偏好信息一致性、群体共识性及残缺元素补全问题展开了深入探讨,采用以粒子群优化算法为代表的智能算法对所建立的模型进行求解。通过一系列研究,取得了如下主要结论:
(1)建立了互补型偏好信息的序列模型,解决了既有研究中偏好信息给出过程的缺失问题。这一模型基于备选方案成对比较过程的复杂性和序列性,完整刻画了决策者在给出偏好信息过程中复杂的决策行为,成为决策分析新的理论基础。在此基础上进行推广,建立了残缺互补型偏好信息的序列模型。
(2)在个体偏好信息一致性改进方面,发现基于互补型偏好信息的序列模型能有效识别需要修改的元素。在此基础上,针对不同类型的个体偏好信息不一致性(包含加型不一致性、积型不一致性和不具有弱传递性)建立了相应的优化模型。此外,还提出基于柔度的模拟方法提高个体偏好的加型一致性。比较分析表明,本文提出的方法不仅使得修正后的互补型偏好信息具有满意一致性而且还尽可能保存了初始偏好信息。
(3)在共识一致性改进方面,对于群体决策问题主要基于迭代和优化两种方法。从迭代的角度,设计了一个共识达成的迭代算法,保证修正后的个体偏好依然具有满意加型一致性。从优化的角度,构建了一个能够同时提高加型一致性和群体共识性的优化模型,其中保证了个体偏好中方案之间的偏好关系不变。同时,对于大规模群体决策问题,主要基于优化的方法。对专家进行子群划分,多指标综合考虑确定专家和子群权重,细致刻画子群的共识水平并建立了相应地群体决策模型。比较分析表明,本文提出的共识方法,能有效提高群体共识水平,促进群体达到满意的决策结果。
参考文献(略)
