本文是一篇计算机论文,本文提出结合对称比与距离比的离群点检测算法,并设计了一种基于最小生成森林(MSF)的新型分裂-合并聚类算法。
第1章 绪论
1.1 引言
进入21世纪,随着信息技术的飞速发展,人类社会逐渐迈入了以数据为核心的数字化时代。互联网的普及、移动设备的广泛使用,以及物联网(IoT)和云计算技术的迅速兴起,使得数据的生成和积累呈现出前所未有的规模和速度。全球数据量的增长趋势异常显著,根据国际数据公司(IDC)的统计,2020年全球数据总量达到64ZB,预计到2025年,这一数字将突破180ZB。数据的形式日趋多样化,不仅包括传统的结构化数据,如企业生产记录和金融交易数据,还涵盖了大量的非结构化数据,如社交媒体动态、图像、视频和传感器生成的数据流。这种数据的海量性、复杂性和动态性为人类的认知和决策带来了前所未有的机遇和挑战。
在数据挖掘技术的众多方法中,聚类分析作为一种无监督学习技术,因其无需预先定义标签的特点,特别适合处理未知模式的问题。聚类的核心目标是根据数据点之间的相似性或距离,将数据集分割为多个子集(簇),以确保同一子集内的数据尽可能具有较高的相似度,而不同子集间的数据则尽量保持较大的差异性。这种基于相似性进行分割的非监督模式识别方法,使得聚类技术在众多领域发挥了重要作用。例如,在图像处理领域,聚类技术可以帮助实现图像分割和目标检测;在文本分析中,聚类可以用于自动主题识别和文档分组;在生物信息学领域,研究人员可以利用聚类技术分析基因的表达规律以及蛋白质的功能特征;在社交网络分析中,聚类被用来发现用户群体和社区结构。
....................
1.2 课题研究现状
1.2.1 离群点检测算法的研究现状
数据驱动的离群点检测在过去十年中得到了广泛研究。Chandola等人[5]在机器学习方法盛行之前对各种类型的离群点和检测方法进行了分类。随后,有多人研究了基于深度学习的离群点检测[6,7]。还有一些针对特定领域的离群点检测调查,例如基于深度学习的图像和视频离群点检测算法、网络流量[8,9]、实时数据[10-12]、城市交通[13]等。在另一项最近的调查中,Samariy[14]等人回顾了52种算法,并根据统计、密度、距离、聚类、隔离、集成等方法对它们进行了分组。尽管这些工作提供了丰富的离群点检测技术概览,但它们并未通过实证研究深入探讨这些方法的有效性和局限性。
现有的离群点检测系统已经使用了统计方法、机器学习算法和领域特定技术的组合。Kotsiantis[15]等人利用工业数据的离群点检测研究表明,监督式离群点检测在处理稀少的离群点标签、适应新的机器类别以及复杂机械方面面临挑战。基于规则的分类方法可能难以应对未见过的模式,而集成技术在内存和高维数据方面存在局限性。依赖静态阈值的离群点检测系统难以适应包含演变模式的动态数据,导致较高的误报率和漏检离群点。为了解决这些问题,越来越多的研究转向无监督和半监督学习方法。
有监督式离群点检测是一种依托标签信息建立分类模型的方法,通过学习正常数据与离群点的区别来识别异常点。具体而言,该方法将离群点检测归为典型的二分类任务,其中“正常点”与“离群点”作为两类。由于有明确的标签信息支持,有监督方法在模型训练过程中可以最大程度地利用数据特征,并通常具有较高的检测精度。有监督方法依赖于明确的正常点和离群点标签,能够利用这些标签构建清晰的分类边界。模型在训练过程中通过最小化误差(如交叉熵或均方误差)学习样本的特征分布,使得正常样本和离群样本的区分更加准确。例如,在金融欺诈检测中,标注的正常交易和欺诈交易可以帮助模型构建精准的分类器。而且有监督方法可以使用各种经典和现代的机器学习模型。例如,SVM[16]可在高维空间建立优化分类边界的超平面;随机森林集成多棵决策树提升识别准确性;深度学习模型如卷积神经网络(CNN)增强特征提取能力,在处理图像异常检测时表现优异[17]。
.........................
第2章 已有聚类算法概述
2.1 基于分区的聚类算法
分区聚类方法一般通过优化特定的聚类准则函数,将数据集直接划分成若干个子类,这类算法的特点是结构清晰、计算简单且效率高,在实际应用中广受关注。然而,分区聚类算法的性能往往受到预设聚类数K的显著影响,且其在非球形分布的数据集上表现较差,仅在球形分布的数据集上能够实现较为理想的聚类效果。
K-means算法是一种常用的分区聚类方法。其过程是首先随机选取K个初始聚类中心,然后根据样本到聚类中心的距离,将每个样本分配到最近的簇中,再根据新的簇内数据分布更新聚类中心位置。该算法反复迭代上述步骤,直到聚类结果稳定不再变化为止。
K-means算法以其简单且高效的特性而广受欢迎,然而该算法也存在一定的缺点,例如聚类中心的初始位置选择会直接影响最终聚类效果。当初始的聚类中心选取在数据分布较为稀疏或偏离簇中心的区域,可能导致部分簇为空或者聚类结果陷入局部最优解。通常情况下,多次运行K-means并从中选取最优结果能够减小这一问题,但会增加计算成本。其次,K-means对非球形簇的适应性较差。该算法该算法通常假定数据集中的各个簇都呈现类似球形的分布,而实际数据中的簇形状往往更加多样和复杂,这会限制其在某些场景下的效果。此外,由于初始聚类中心的选择具有随机性,每次运行K-means都可能产生不同的聚类结果,从而使得算法结果具有一定的不确定性。
.........................
2.2 基于层次的聚类算法
与分区聚类不同,层次聚类通常通过逐步合并或分裂数据对象构建树状结构。在该结构中,每层聚类的细粒度不同,可依据需求选择合适层级。该方法主要分为两类:自底向上的凝聚式聚类与自顶向下的分裂式聚类。前者从每个数据点作为单独的簇开始,通过逐步合并相似度最高的簇,直到达到目标的簇数量为止;后者则从整体出发,将所有数据作为一个簇,通过逐步分裂成多个子簇,直到达到预期的聚类数量。
AGNES算法[46]是一种典型的凝聚式层次聚类方法。该算法起初将每个数据点作为一个独立的簇,然后反复合并两个最相似的簇,直到所剩簇的数量等于给定的目标数K为止。具体过程如下所述:

计算机论文怎么写
.................................
第3章 已有的离群点检测算法 ....................... 24
3.1 监督离群点检测算法 .................................... 24
3.2 无监督离群点检测算法 .................................. 25
3.3 本章小结 ........................................ 26
第4章 基于对称比和距离比的离群点检测算法 ..................... 27
4.1 基于对称和距离比的离群点检测算法 ........................... 27
4.2 算法流程和解释 ................................ 29
4.3 时间复杂度分析 .............................. 30
第5章 分裂-合并聚类算法 ......................... 32
5.1 常见的分裂算法 .................................. 32
5.1.1 基于划分的分裂算法 ......................... 32
5.1.2 基于k近邻的分裂算法 ........................ 33
第7章 实验结果及分析
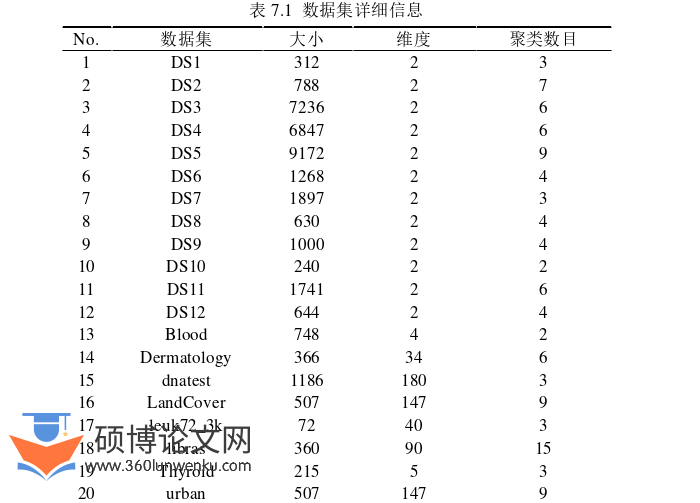
7.1 实验设置
实验设计的27个数据集的详细信息如表7.1所示。数据集1-12是12个二维合成数据集,将会在7.2节中详细介绍。数据集13-27是15个真实数据集,其中数据集13-22来自UCI。相较于数据集13-22,数据集23-27具有更高的维度。
计算机论文参考
............................
第8章 全文总结与展望
8.1 本文工作总结
(1) 本文提出一种全新无监督离群检测算法。针对现有方法依赖标签且稳定性不足的问题,提出新的检测策略,主要基于两点假设:离群点是远离于大部分的正常数据点,它们的对称性差;正常数据点与其近邻的近邻的距离是相近的。在此基础上,本文提出了一种基于对称性与距离比的离群点检测算法。首先,构建数据集的k近邻图;接着,分别计算数据点的对称比和距离比;然后,利用对称比和距离比相减来度量数据点的离群度;最后,利用四分位法自动获得离群点的阈值。相比一些有监督或无监督算法,本文的算法在实验中的准确率较高。
(2) 提出了一种新的聚类算法。针对基于k近邻与MST的聚类方法在构建数据图结构时的潜在缺陷,如无法获取连通图或数据局部结构等,本文提出一种基于最小生成森林的聚类算法。首先,构建最小生成森林以获取数据图结构;其次,在生成过程中计算相关图信息,如每个数据点的密度变化率;接着,从任一点出发沿着密度变化率最大的方向搜索,直到簇中心点为止,分裂数据集;然后,根据小簇的规模和结构以及在最小生成森林中的连接结构进行初步的小簇合并;最后,计算新的簇间距离,不断合并小簇直到K个簇为止。本算法在二维数据集和真实数据集的结果表明,本文提出的聚类算法在相比较的聚类算法中性能较优。
参考文献(略)
