第一章 绪论
1.1研究背景
生存分析是统计学的一个重要且活跃的分支,它在许多学科和生产生活中都有着广泛的应用和迅速的发展,例如医学、经济学、教育学、生物学、人口统计学、工业、金融以及保险行业等等[1]。上述领域中都存在着对某给定事件(也被称为感兴趣事件)发生的时间进行预测的问题。这类研究事件发生时间的规律问题都能够运用生存分析来解决,再加上生存分析还能够解决生活中常见的截断数据问题,所以自从上世纪 70 年代起,生存分析就得到了研究人员的高度重视,以及迅猛发展。
生存分析主要研究以下三个方面的内容[2]:一是研究事物的生存过程,例如分析人群生存状况所包含的规律,计算在某个时间节点的生存率的变化趋势等;二是比较生存过程,通过比较个体的生存率的标准误差,进而可以分析比较各个组之间的生存过程是否具有显著的差异;三是研究对象的生存时间,即估计研究目标在某些感兴趣状态下的持续时间,例如临床治疗中患者的死亡时间,疾病的发生时间[3],失业和再就业时间,犯人的假释时间,机械系统的器件失败时间[4]或客户行为分析中用户的购买时间[5]等。这就需要我们基于生存分析的数据进行数学建模。通常而言,自变量取影响生存时间的各种因素(在医学分析中,往往是病人的微阵列基因表达数据等),因变量取研究目标对应的生存时间。本文主要关注的是如何建立有效的数学模型,从而更好地预测研究目标的生存时间。
生存分析的研究中,我们需要观测研究目标从实验开始到感兴趣事件的发生(如死亡,元器件失效),但在实际应用中,由于研究的时间限制,研究环境条件有限或者研究目标失访等问题,研究人员并不一定能够观察到每个感兴趣事件的发生时间,也就无法将所有的观测目标的完整持续时间全部记录下来,也就是说在观测过程中可能会产生删失数据(censoreddata)[6]。具体而言,删失数据一般可以分成三类[2]:第一类是区间删失数据,即若研究人员无法给出相应研究对象生存时间的精确值,但可以确定事件发生的时间区间,则该类数据称之为区间删失数据;第二类是左删失数据,即若研究人员无法给出生存时间的精确值,但可以确定时间小于或者等于某一具体值;第三类是右删失数据,即若研究人员无法给出生存时间的精确值,但可以确定时间大于或者等于某一具体值。值得注意的是,在上述三种情况下,真正的事件发生时间都是未知的。其中,右删失数据是实际应用中最常见的情况[7]。因此,不失一般性,本文主要关注右删失数据的相关案例。
......................
1.2研究现状
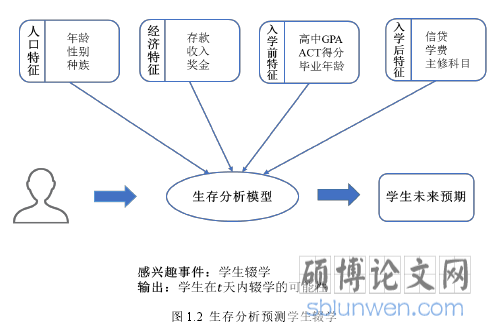
作为统计学领域的一个重要的分支领域,生存分析在许多领域都有着广泛应用,如医药、生物、教育、金融和工业等等。由于生存分析能够妥善地解决实际应用中常见的删失数据问题,同时还能推动数理统计学的发展,所以受到了国内外研究者的高度关注,并且提出了各种有效的生存分析模型以及适应现实需求的各类扩展方案。例如,在教育领域,Ameri 使用生存分析来预测学生辍学后的返校时间[15];在金融领域,Li 则用来预测众筹项目会在什么时间段内取得成功[14]。如下所示,图 1.2 直观地展示了如何使用生存分析模型来预测学生的辍学几率。
通常来说,研究人员一般将生存分析模型划分成两大类别——统计类生存方法以及基于机器学习的生存分析方法[16]。无论是统计类模型或者是基于机器学习模型,它们的主要目的都是预测生存时间或者估计生存时间内感兴趣事件的生存概率。当然,这两类模型所基于的理念是不相同的。具体来说,传统的统计学习模型主要是通过估计生存曲线来描述事件时间的分布和参数的统计特性,而且这些模型通常用于处理低维数据。另一方面,基于机器学习的生存分析模型往往会将传统的生存分析方法与各种最新的机器学习理论相结合,以不同的方式学习协变量与生存时间之间的依赖关系,从新的角度出发来预测感兴趣事件的发生。相较于单一的统计类模型,它们往往能够提供有效的解决算法,也能够更加有效地处理高维数据问题。
............................
第二章 课题研究基础
2.1最大期望算法
本节主要介绍最大期望算法(Expectation-Maximization algorithm,EM),以及 EM 算法在估计高斯混合模型的参数方面的应用。
2.1.1EM 算法简介
当概率模型(例如高斯混合模型)中即包含观测到的变量,同时又存在隐含变量(观测变量对应的潜在的变量)时候,那么对于样本数据,我们无法通过极大似然估计算法来估计出概率模型中的各项参数。此时,我们需要引入一种迭代类型的优化算法进行参数的估计与求解——EM 算法[52,53]。最大期望算法主要用于处理样本数据缺失的模型参数估计类问题,与此同时,当样本数据中存在隐变量的时候,这类问题也可以归属于数据缺失类问题,即可以将其视为数据缺失了各个样本所归属的类别。它的核心思想是:将极大化似然函数的过程分解成为多步迭代的过程,通过逐步增大似然函数值的方式估计参数。最大期望算法之所以称为 EM 算法,主要是因为该算法可以分为以下两大步骤:E-step(expectation-step,期望步)以及M-step(Maximization-step,最大化步)。其中 E 步用于在上一轮求解的基础上,计算对数似然函数对于隐变量的条件期望,M 步则是用来极大化期望,从而更新参数估计值。
......................
2.2贝叶斯优化
值得注意的是,很多上述的实际问题都存在着大量复杂的决策,同时优化目标可能存在多峰、非凸、高维或者是决策空间巨大等等这些挑战。此外,这些优化目标还有着“黑箱”以及评估代价高昂等一系列的困难,也就是说优化目标可能无法使用较为明确的数学表达式来描述,甚至有时为了得到所需要解决问题的结果,还得耗费巨大的代价。例如:在药物配置中,如果将药物的配方当做决策空间,药物的治疗效果当做优化的目标函数。在该问题中,需要通过不断地配置各种各样的药物,进行实验,从而找到最优的治疗配方来治愈病人。显而易见,想要评估每种配方的效果所需要的代价是相当大的,有的配方甚至会导致病人的病情进一步恶化。
为了解决上述难题,我们可以选择使用一种较为优秀且通用的优化算法框架——贝叶斯优化算法(BayesianOptimization,BO)[54]。贝叶斯优化还有着其他几种称呼方式,例如可以称其为高效全局优化(EfficientGlobalOptimization,EGO)或者是序贯克里金优化(SequentialKrigingOptimization,SKO)等等。贝叶斯优化是一种非常有效的全局优化算法,主要应用于模型的序贯决策问题,即通过很少的评估能够得到对应问题的近似最优解。该算法已经成功地应用于自动机器学习[55],材料设计[56],推荐系统[57]和传感器网络[58]等等,并且获得了优异的成果。贝叶斯优化之所以能够通过较少的次数评估从而得到近似最优解,关键在于它使用了关于对应问题的先验信息以帮助指导采样,并权衡搜索空间的探索和开发。具体来说,贝叶斯优化首先使用代理模型来拟合所要解决的目标函数(具体问题),然后根据拟合的结果和相应的规则选择出下一个最具有“潜力”的评估点进行“开采”,所以贝叶斯优化能够避免冗余的采样和高昂的代价。此外,贝叶斯优化还能够利用过往的采样信息,即完整的历史信息,从而能够较为有效地提高算法探索和开采的效率,并且避免了庞大的计算量。
..............................
第三章 先验信息引导的直推式矩阵补全生存分析模型............................... 25
3.1问题建模.............................. 26
3.1.1 生存分析问题描述 ...................................... 27
3.1.2 先验信息引导的直推式矩阵补全模型........................... 28
第四章 噪声容错弱监督矩阵补全生存分析模型........................................ 41
4.1问题建模.......................... 42
4.1.1 生存分析问题阐述 ....................... 42
4.1.2 噪声容错弱监督矩阵补全模型............................ 42
第五章 总结与展望................................. 54
5.1工作总结........................... 54
5.2研究展望..................................... 55
第四章 噪声容错弱监督矩阵补全生存分析模型
4.1问题建模
类似于上一章节,本小节依旧基于多任务直推式矩阵补全的思路再次对生存分析进行建模。同时通过利用混合高斯分布来拟合数据中各类未知复杂的噪声,来帮助模型进一步提高生存分析预测性能。
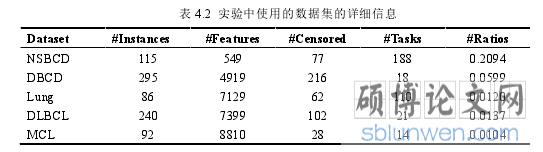
本文使用了五个公开的癌症生存分析数据集,具体包括 Norwegian/StanfordBreastCancerData (NSBCD)、the Dutch Breast Cancer Data (DBCD)、Gene expression profiles of Lungadenocarcinoma (Lung)、Diffuse Large B-Cell Lymphoma (DLBCL)和 Mantle Cell Lymphoma(MCL) 数 据 集 。 这 些 数 据 集 可 以 分 别 从 http://user.it.uu.se/~liuya610/download.html 和http://llmpp.nih.gov/MCL/下载。表 4.2 概述了这些数据集的相关信息,其中“#Instances”列表示数据集所包含的实例数(包括删失和未删失实例),“#Features”列表示相应数据集中实例的特征数,“#Censored”列表示数据集中所含的删失实例数,“#Labels”列表示每个数据集对应的任务个数(也就是所划分的时间间隔数,其中 NSBCD 和 Lung 数据集以“月”作为时间间隔单位,MCL、DBCD 和 DLBCL 数据集以“年”作为时间间隔单位)。此外,为了表明所采用的数据集是否为高维小样本问题,我们还在“#Ratios”列记录了每个数据集中实例数与特征数之间的比例,通常认为当样本个数比特征维数低一个数量级时即为高维小样本问题,按照这个标准,我们容易发现表 4.2 中后四个数据集都属于高维小样本问题。数据集简要介绍如下表 4.2 所示。
...........................
第五章 总结与展望
5.1工作总结
针对上述问题,本文将最初的生存分析问题建模为多任务直推式矩阵补全问题。在此基础上,递进地提出了两种不同的矩阵补全模型,并对这些模型进行了优化求解,有效地克服了上述种种不足。
论文完成的具体研究内容如下:
1)本文充分调研了生存分析领域国内外的研究现状,同时调研了其中各类常用的生存分析算法、公开的微阵列基因表达数据集和通用的评价指标。从广义上说,生存分析方法可以分为两大类:统计类生存分析方法以及基于机器学习的生存分析方法。统计类的生存分析模型主要包括 Cox 比例风险回归模型和参数删失回归模型。而基于机器学习的生存方法中,多任务学习的方法效果比较好。此外,本文还详细介绍和分析了这些模型的设计思路和它们存在的缺陷之处。
2)针对生存分析中高维删失数据所固有的数据标记不完整及高维小样本导致的过拟合缺陷,提出一种先验信息引导的直推式矩阵补全模型(PigTMC)。具体来说,基于特征矩阵潜在的低秩性质以及特征与对应生存状态之间的线性依赖性假设,本文将生存分析问题建模成多任务直推式矩阵补全(Multi-taskTransductiveMatrixCompletion,MTMC)问题。因为 MTMC模型是一个直推式的学习模型,它不仅可以利用删失的实例来弥补样本小的问题,而且还可以探索训练样本和测试样本的特征分布,有利于提高模型在测试样本上的泛化性能。此外,本文在原先的 MTMC 模型上加入了一种新颖的多任务直推式的特征选择方案,来帮助模型缓解过拟合问题。与一般的多任务学习方法不同,本文是在去噪的特征空间而不是原始特征空间上进行特征选择。另外,本文还利用了相邻时间间隔生存状态的先验信息——时序稳定性来指导模型进行生存分析。此外,本文设计了一种基于块坐标下降法的优化算法来解决PigTMC 模型,这种算法能够保证模型的收敛性。最后,本文在 5 个真实数据集上进行了实验,结果显示 PigTMC 模型在 C-index 和加权平均 AUC 指标上表现很出色。
参考文献(略)
