第一章 绪论
1.1 研究背景
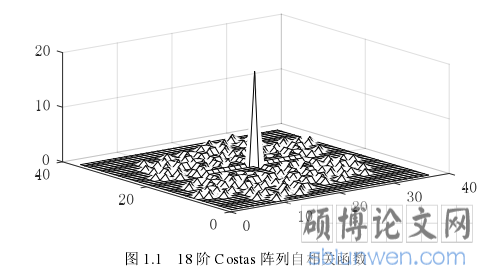
1965 年,J.P.Costas 为了改变声呐系统的性能,在研究设计声呐信号时,提出了一种具有理想自相关性能的信号,即 Costas 阵列[1]。如图 1.1 所示的一个 18 阶 Costas 阵列的自相关函数,其主峰高且尖利,同时次峰低且平展(自相关函数类似“图钉状”),由于其理想的自相关特点[2],对象接近或者偏离的速度可以精确地判定 [3],因此 Costas 阵列已普遍运用无线通信、雷达和遥测等领域 [4]。另外由于它的非循环相关特性很好,非线性特性强。在多值逻辑、密码学等领域中也有一定的应用[5]。
......................
1.1 研究背景
1965 年,J.P.Costas 为了改变声呐系统的性能,在研究设计声呐信号时,提出了一种具有理想自相关性能的信号,即 Costas 阵列[1]。如图 1.1 所示的一个 18 阶 Costas 阵列的自相关函数,其主峰高且尖利,同时次峰低且平展(自相关函数类似“图钉状”),由于其理想的自相关特点[2],对象接近或者偏离的速度可以精确地判定 [3],因此 Costas 阵列已普遍运用无线通信、雷达和遥测等领域 [4]。另外由于它的非循环相关特性很好,非线性特性强。在多值逻辑、密码学等领域中也有一定的应用[5]。

......................
1.2 国内外研究现状
20 世纪 80 年代,S.W.Golomb 等人将伽罗瓦域的数学理论引入到 Costas 阵列的构造研究中并取得重大的突破,构造出了 Welch Costas 阵列和 Golomb Costas 阵列[8-12]。由此 Costas阵列的研究再次引起国内外学者的重视,并取得了一定的研究成果,已提出的一些构造 Costas阵列的代数方法有: Welch 构造法、Golomb 构造法和 Lempel 构造法等[13,14],此外还可以通过已经获得的高阶 Costas 阵列去掉特定的行和列得到新的低阶 Costas 阵列。以及一些特殊的增长构造法:如利用代数方法求出的第一、第二增长构造法及对角落加点的第三增长构造法,不过还没有找到一般的增长构造法[15]。
从 2006 年至今,以 Drakaris、Richard 和 James Beard 领导的研究团队一直致力于 Costas阵列的搜索研究[16-22]。目前该团队已经搜索发现 29 阶的 Costas 阵列的存在,但是其团队并未公布具体算法,只是发布了搜索结果[20]。近几年该研究团队重点研究 Costas 阵列搜索的并行算法。
20 世纪 80 年代,S.W.Golomb 等人将伽罗瓦域的数学理论引入到 Costas 阵列的构造研究中并取得重大的突破,构造出了 Welch Costas 阵列和 Golomb Costas 阵列[8-12]。由此 Costas阵列的研究再次引起国内外学者的重视,并取得了一定的研究成果,已提出的一些构造 Costas阵列的代数方法有: Welch 构造法、Golomb 构造法和 Lempel 构造法等[13,14],此外还可以通过已经获得的高阶 Costas 阵列去掉特定的行和列得到新的低阶 Costas 阵列。以及一些特殊的增长构造法:如利用代数方法求出的第一、第二增长构造法及对角落加点的第三增长构造法,不过还没有找到一般的增长构造法[15]。
从 2006 年至今,以 Drakaris、Richard 和 James Beard 领导的研究团队一直致力于 Costas阵列的搜索研究[16-22]。目前该团队已经搜索发现 29 阶的 Costas 阵列的存在,但是其团队并未公布具体算法,只是发布了搜索结果[20]。近几年该研究团队重点研究 Costas 阵列搜索的并行算法。
文献[23]提出了一种 Costas 阵列穷举搜索算法,该算法采用回溯法遍历得到置换矩阵,然后计算获得置换矩阵对应的差异矩阵,并将其作为判定准则,只有差异矩阵中每一列都不存相同的元素时才是 Costas 阵列,从而实现对 Costas 阵列的搜索。文献[24]提出了一种利用GPU 和 FPGA 硬件加速 Costas 阵列搜索的方法,由于其算法本质上同样是基于差异矩阵来实现的,因此虽然搜索速度得到了提高,但是并不显著。
文献[25]同样基于伽罗瓦域的数学概念创立了具有一个空隙行的 Welch Costas 阵列结构。同时探索了将其应用于OFDM无线通信系统中来解决多普勒频移问题以及设计和分派跳频码的问题。文献[26]通过循环移位法研究具有一个空隙行和一个空隙列的 Golomb Costas 阵列,
文献[25]同样基于伽罗瓦域的数学概念创立了具有一个空隙行的 Welch Costas 阵列结构。同时探索了将其应用于OFDM无线通信系统中来解决多普勒频移问题以及设计和分派跳频码的问题。文献[26]通过循环移位法研究具有一个空隙行和一个空隙列的 Golomb Costas 阵列,
同时研究了用其设计 OFDM 系统中跳频模式。
..........................
第二章 Costas 阵列简介
2.1 置换矩阵
置换矩阵的表示 置换矩阵的表示方法主要有两种,即矩阵表示与列定位值表示。以阶数是 3 的置换矩阵为例,三阶置换矩阵总个数为 6。
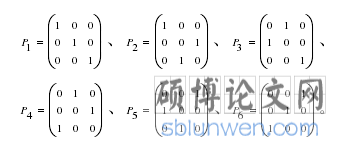
这 6 个置换矩阵的矩阵表示方式如下所列:
..........................
第二章 Costas 阵列简介
2.1 置换矩阵
置换矩阵的表示 置换矩阵的表示方法主要有两种,即矩阵表示与列定位值表示。以阶数是 3 的置换矩阵为例,三阶置换矩阵总个数为 6。
这 6 个置换矩阵的矩阵表示方式如下所列:

矩阵表示法直观明了,但是对于高阶置换矩阵书写不便,同时在利用算法搜索实现中需要大量计算机内存来存储置换矩阵的所有位置上的元素,而其中大部分位置上的元素都是 0,这样会导致浪费大量的内存,降低算法速度,不利于编程搜索。
......................
2.2Costas 阵列的获得
获得 Costas 阵列的方法主要有两种:伽罗瓦域构造法和枚举搜索法,伽罗瓦域构造法和枚举搜索法各有优劣,下面重点分析这两种方法,并进行比较。
2.2.1伽罗瓦域构造法
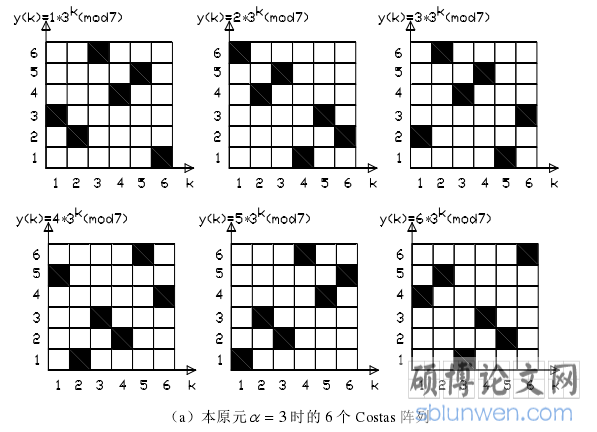
Costas 阵列的伽罗瓦域构造方式是基于伽罗瓦域理论[37],将伽罗瓦域中的本原元和非零元,代入到相应的放置函数中,即可获得 Costas 阵列[38]。伽罗瓦域构造方式相对比较简单,可以快速地构建出一个 Costas 阵列。伽罗瓦域构造法有两种方法:Welch 结构和 Golomb 结构。
 ..............................
..............................
2.2Costas 阵列的获得
获得 Costas 阵列的方法主要有两种:伽罗瓦域构造法和枚举搜索法,伽罗瓦域构造法和枚举搜索法各有优劣,下面重点分析这两种方法,并进行比较。
2.2.1伽罗瓦域构造法
Costas 阵列的伽罗瓦域构造方式是基于伽罗瓦域理论[37],将伽罗瓦域中的本原元和非零元,代入到相应的放置函数中,即可获得 Costas 阵列[38]。伽罗瓦域构造方式相对比较简单,可以快速地构建出一个 Costas 阵列。伽罗瓦域构造法有两种方法:Welch 结构和 Golomb 结构。

第三章 基于向量的 Costas 阵列搜索算法 ................................... 15
3.1 置换矩阵生成 ......................................... 17
3.2 Costas 阵列判断准则优化 ........................................ 18
3.3 算法思想 ................................... 20
第四章 Costas 阵列搜索算法的优化 ........................................ 23
4.1 链表 ........................................... 23
4.1.1 单向链表 ..................................... 23
4.1.2 单向循环链表 ........................................ 25
第五章 Costas 阵列并行搜索 ............................................. 35
5.1 并行程序设计基础 ........................................ 35
5.1.1 并行编程范式 ....................................... 35
5.1.2 进程和线程 .................................35
第五章 Costas 阵列并行搜索
5.1 并行程序设计基础
并行程序设计,许多并行代码并不存在于所需的应用程序中;即使存在某个并行代码,它也无法运行在用户特定的并行机器上,原因是并行代码最初是针对各种具体的并行结构编写的。虽然并行编程中还存在大量问题,但是取得的进步是显著的。主流并行程序设计模型主要有 3 类:数据并行(如 HPF),消息传递(如 MPI 和 PVM)和共享变量(如 OpenMP)。
5.1.1 并行编程范式
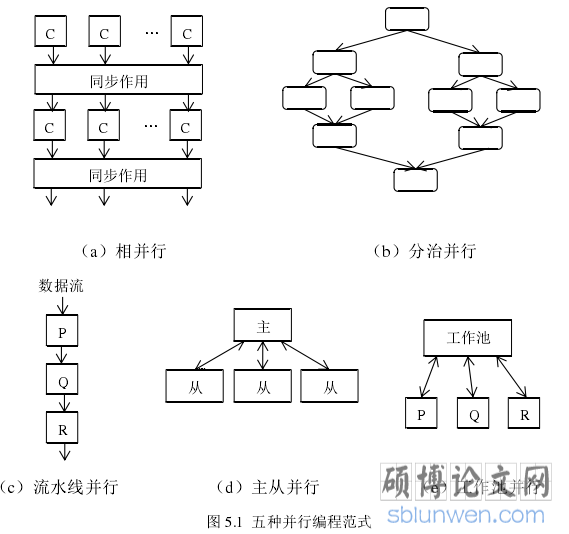
所谓并行编程范式(Parallel Programming Paradigms)是指实现并行算法的方法。现在已经提出好几种方式,这些并行编程范式不仅能够独立使用它们,而且将它们混合在一起使用也是可以的。参照图 5.1,现分述如下[52-61]。
并行程序设计,许多并行代码并不存在于所需的应用程序中;即使存在某个并行代码,它也无法运行在用户特定的并行机器上,原因是并行代码最初是针对各种具体的并行结构编写的。虽然并行编程中还存在大量问题,但是取得的进步是显著的。主流并行程序设计模型主要有 3 类:数据并行(如 HPF),消息传递(如 MPI 和 PVM)和共享变量(如 OpenMP)。
5.1.1 并行编程范式
所谓并行编程范式(Parallel Programming Paradigms)是指实现并行算法的方法。现在已经提出好几种方式,这些并行编程范式不仅能够独立使用它们,而且将它们混合在一起使用也是可以的。参照图 5.1,现分述如下[52-61]。
.........................................
第六章 总结与展望
论文在简要介绍Costas 阵列的由来,了解阵列相关知识的基础上,讨论了两种获得 Costas阵列的方式,即伽罗瓦域构造方式和枚举搜索方式。论文讨论了这两种方式的优劣,其中着重研究了 Costas 阵列的枚举搜索算法。
本文针对基于差异矩阵的枚举搜索算法存在的缺陷,提出了一种基于向量的 Costas 阵列搜索算法。首先,在判断置换矩阵的同时判断该置换矩阵是否符合 Costas 阵列判断准则,克服了回溯法遍历所有置换矩阵的缺点,去除了不必要的计算,降低了冗余。其次,利用 Costas阵列自身特点,提出了新的基于向量的 Costas 阵列判别准则来判别一个置换矩阵是否为Costas 阵列。即在任意一个 Costas 阵列中没有两个相同的向量。基于向量的算法简化了判决准则,优化了搜索程序,降低了时间复杂度,使得搜索速度得到极大地提升。通过研究双向循环链表和 Costas 阵列的结构特性,利用双向循环链表可以方便的解决生成置换矩阵时多次判断与前几行是否冲突的问题,避免了每次都要与前面的行进行判断比较,有利于程序搜索速度的提升。其次利用 Costas 阵列之对称性来进一步简化搜索程序,加速搜索过程。最后研究了 Costas 阵列的并行搜索,通过并行程序进一步加速阵列的搜索过程,使得搜索高阶 Costas阵列也变为可能。
本论文主要研究 Costas 阵列的枚举搜索算法以及并行搜索程序,而并行搜索程序依赖于单机性能。在未来的研究中可以进一步研究多机并行搜索,在多机并行搜索中需要将多台计算机通过网络连接以一定的方式有序的组织起来。而这又需要解决网络的连接方式、计算机网络之间通信方式、操作系统、中间件等问题。此外还需研究解决子任务的划分以及各个计算机节点之间的通信协作问题。
参考文献(略)
