第一章 绪论
1.1 研究背景与意义
近年来,随着互联网和移动端的崛起,数据的来源越发多样,这使得数据内容变得丰富且体积庞大。数据本身包含大量信息,且数据的维度也随之增长。维度较高的数据给模型的训练带来了困难,极大地限制了模型的上限。如何寻找到高维数据的低维表示是当前机器学习研究领域中的热点研究方向之一。在众多的相关研究中,潜特征模型(Latent Feature Model,LFM)凭借其简单的形式和方便地计算成为处理这一问题的有效方法之一,在文档和图像等海量数据的建模和分析中得到了广泛的应用。
潜特征模型通过一系列潜在特征的线性组合来表示高维数据,对特征的不同假设,产生了不同的潜特征模型,如因子分析(Factor Analysis,FA)[1][2]、主成分分析(Principal Component Analysis,PCA)[3][4]和独立成分分析(Independent Component Analysis,ICA)[5][6]等。潜特征模型中的一个关键问题是如何选择特征的数目。一般的做法是预先假设模型中潜在特征的数目,显然这种方法不能很好地适应数据(特征的数量不能随着数据的改变而自适应改变)。另一种做法是使用贝塔过程,它可以随着模型内数据的改变而自适应改变特征的数量。
贝塔过程一种非参数贝叶斯模型,可以理解为是无限维参数空间上的贝叶斯模型,其结合了非参模型和贝叶斯理论,为使用非参数方法的模型提供了模型选择和贝叶斯框架[7]。在潜特征模型中使用贝塔过程,模型可以从数据中推断出潜特征的数量,且随着数据量的改变特征的数量也自适应变化。追随贝塔过程的思想,研究者们不断探索贝塔过程在潜特征模型中的应用。
........................
1.2 研究现状
传统的非参数贝叶斯模型中都存在数据可交换性这一假设。在非参数贝叶斯领域中,依赖的想法最早出现于狄利克雷过程中,使用依赖信息去除数据可交换的假设,并以此为起点逐渐发展开来。研究者们使用一种协变量表示数据之间的依赖信息,将其引入到贝叶斯模型中,提出依赖的贝叶斯模型,从而去除了贝叶斯模型中的不可交换性。协变量是存在于数据之间的依赖信息,例如空间数据中的位置信息或时序数据中的时间信息。借助协变量,研究者们不断的探索依赖信息在各类非参数贝叶斯模型中的应用。本小节首先介绍了依赖的非参贝叶斯模型的相关研究,随后具体介绍了依赖的贝塔过程的相关研究。
1.2.1 依赖非参贝叶斯模型的相关研究
文献[12]中分析依赖的思想并提出依赖的狄利克雷过程(Dependent dirichlet process, DDP)。文献[13]从构造的角度出发提出了一种构造 DDP 的新方法,并且使用吉普斯采样方法推导该模型。文献[14]中将依赖的狄利克雷混合模型与对象和位置模型相结合,提出依赖的狄利克雷混合对象模型(Dependent Dirichlet process mixture of objects,DDPMO)用于视频的中任意对象的查找,跟踪和表示。文献[15]扩展了依赖的狄利克雷过程,使用高斯过程来捕获数据之间位置的依赖信息,提出位置依赖的狄利克雷过程( Location dependent dirichlet processes,LDDP),并将其用于图像修复。随后,Williamson 等人将依赖信息引入到印度自助餐过程中,提出依赖的印度自助餐过程(Dependent Indian Buffet Process,DIBP)[16],使用分层高斯过程来解释协变量的依赖,协变量通过核嵌入到协方差矩阵中。
........................
1.2 研究现状
传统的非参数贝叶斯模型中都存在数据可交换性这一假设。在非参数贝叶斯领域中,依赖的想法最早出现于狄利克雷过程中,使用依赖信息去除数据可交换的假设,并以此为起点逐渐发展开来。研究者们使用一种协变量表示数据之间的依赖信息,将其引入到贝叶斯模型中,提出依赖的贝叶斯模型,从而去除了贝叶斯模型中的不可交换性。协变量是存在于数据之间的依赖信息,例如空间数据中的位置信息或时序数据中的时间信息。借助协变量,研究者们不断的探索依赖信息在各类非参数贝叶斯模型中的应用。本小节首先介绍了依赖的非参贝叶斯模型的相关研究,随后具体介绍了依赖的贝塔过程的相关研究。
1.2.1 依赖非参贝叶斯模型的相关研究
文献[12]中分析依赖的思想并提出依赖的狄利克雷过程(Dependent dirichlet process, DDP)。文献[13]从构造的角度出发提出了一种构造 DDP 的新方法,并且使用吉普斯采样方法推导该模型。文献[14]中将依赖的狄利克雷混合模型与对象和位置模型相结合,提出依赖的狄利克雷混合对象模型(Dependent Dirichlet process mixture of objects,DDPMO)用于视频的中任意对象的查找,跟踪和表示。文献[15]扩展了依赖的狄利克雷过程,使用高斯过程来捕获数据之间位置的依赖信息,提出位置依赖的狄利克雷过程( Location dependent dirichlet processes,LDDP),并将其用于图像修复。随后,Williamson 等人将依赖信息引入到印度自助餐过程中,提出依赖的印度自助餐过程(Dependent Indian Buffet Process,DIBP)[16],使用分层高斯过程来解释协变量的依赖,协变量通过核嵌入到协方差矩阵中。
.......................
第二章 相关知识介绍
2.1 贝塔过程
贝塔过程最初是在统计领域中的研究[21][22],在文献[23][24]中将其引入到机器学习领域,并将其用于潜特征模型中。它可以产生一系列带有权值为 0 到 1之间的原子,因此贝塔过程以及其相关的变体过程可以参数化伯努利过程,从而产生稀疏的二值矩阵。除此之外,也有大量的研究将其作为先验引入到隐马尔可夫模型中,如文献[25][26][27]。
2.1.1 贝塔过程的构造方法
目前贝塔过程常用三种构造方法:1)印度自助餐构造方法;2)有限近似的方法;3)折棍构造方法。下面简单地介绍印度自助餐过程以及有限近似,贝塔过程的折棍构造将在第三章中进行详细地解说。
贝塔过程中假设数据是可交换的,即交换数据的顺序对模型的推导不造成影响。但是大多数情况,例如时序数据或空间数据,这些数据样本在时间或者空间相近的地方,有相似的结构。非参贝叶斯数模型中的可交换性会打破数据上存在的依赖信息,从而获取不到隐藏在数据中的依赖信息。
如何捕捉到数据之间的依赖信息呢?为了解决这个问题,在非参贝叶斯模型中引入协变量,用协变量刻画数据之间的依赖信息(时间或空间信息)。将协变量整合到模型中,从而达到去除数据可交换性的目的。随着这一想法地提出,研究者们对引入协变量去除可交换性假设的非参贝叶斯模型做了大量的研究[28][29][30][31]。基于以上工作,依赖贝塔过程逐渐引起研究者们的注意并发展。依赖贝塔过程的目的是希望协变量相似的样本数据拥有类似的特征。在本小节介绍几种依赖贝塔过程。
2.2.1 核贝塔过程
首先介绍基于核函数的依赖贝塔过程。在文献[17]中提出一种新的列维过程——核贝塔过程用来学习一组不可数的、具有依赖信息的潜特征模型。通过在传统的贝塔过程中引入依赖信息,使得模型更加适用于带有依赖信息的数据集。每个样本数据带有协变量,且为每个特征学习潜在的协变量信息。
用类似印度自助餐过程来描述核贝塔过程:与印度自助餐过程一样,顾客表示样本数据,菜品表示特征。需要引入协变量l 。L 表示协变量空间。nl 表示第 n个样本数据携带的协变量,是可以观测到的协变量。*kl 是第 k 个特征携带的协变量,它是通过模型学习得到。带有协变量nl 的样本生成过程可以两步过程如表 2-2 所示:

.........................
第二章 相关知识介绍
2.1 贝塔过程
贝塔过程最初是在统计领域中的研究[21][22],在文献[23][24]中将其引入到机器学习领域,并将其用于潜特征模型中。它可以产生一系列带有权值为 0 到 1之间的原子,因此贝塔过程以及其相关的变体过程可以参数化伯努利过程,从而产生稀疏的二值矩阵。除此之外,也有大量的研究将其作为先验引入到隐马尔可夫模型中,如文献[25][26][27]。
2.1.1 贝塔过程的构造方法
目前贝塔过程常用三种构造方法:1)印度自助餐构造方法;2)有限近似的方法;3)折棍构造方法。下面简单地介绍印度自助餐过程以及有限近似,贝塔过程的折棍构造将在第三章中进行详细地解说。
印度自助餐过程:在印度自助餐过程中,样本数据用“顾客”表示,模型中的潜特征用“菜品”表示。假设有 N 个顾客进行就餐,餐厅有无限多的菜品可以供顾客选择,且一个顾客可以选取多个菜,用 0,1 表示第 n 个顾客是选取第k个菜品。一个印度自助餐过程如表 2-1 所示[24]。在文献[23]中讨论了贝塔过程与伯努利过程的关系。并详细地给出了贝塔过程的生成过程。

..........................
2.2 依赖贝塔过程
..........................
贝塔过程中假设数据是可交换的,即交换数据的顺序对模型的推导不造成影响。但是大多数情况,例如时序数据或空间数据,这些数据样本在时间或者空间相近的地方,有相似的结构。非参贝叶斯数模型中的可交换性会打破数据上存在的依赖信息,从而获取不到隐藏在数据中的依赖信息。
如何捕捉到数据之间的依赖信息呢?为了解决这个问题,在非参贝叶斯模型中引入协变量,用协变量刻画数据之间的依赖信息(时间或空间信息)。将协变量整合到模型中,从而达到去除数据可交换性的目的。随着这一想法地提出,研究者们对引入协变量去除可交换性假设的非参贝叶斯模型做了大量的研究[28][29][30][31]。基于以上工作,依赖贝塔过程逐渐引起研究者们的注意并发展。依赖贝塔过程的目的是希望协变量相似的样本数据拥有类似的特征。在本小节介绍几种依赖贝塔过程。
2.2.1 核贝塔过程
首先介绍基于核函数的依赖贝塔过程。在文献[17]中提出一种新的列维过程——核贝塔过程用来学习一组不可数的、具有依赖信息的潜特征模型。通过在传统的贝塔过程中引入依赖信息,使得模型更加适用于带有依赖信息的数据集。每个样本数据带有协变量,且为每个特征学习潜在的协变量信息。
用类似印度自助餐过程来描述核贝塔过程:与印度自助餐过程一样,顾客表示样本数据,菜品表示特征。需要引入协变量l 。L 表示协变量空间。nl 表示第 n个样本数据携带的协变量,是可以观测到的协变量。*kl 是第 k 个特征携带的协变量,它是通过模型学习得到。带有协变量nl 的样本生成过程可以两步过程如表 2-2 所示:

.........................
3.1 贝塔过程的对偶空间字典学习 ................................... 20
3.2 核贝塔过程的对偶空间字典学习 ................................. 22
第四章 变分依赖贝塔过程的构造及推理 ..................... 32
4.1 贝塔过程的折棍构造 ........................................... 32
4.1.1 贝塔过程的原始折棍构造 ................................... 32
4.1.2 贝塔过程的改进折棍构造 ................................... 34
第五章 变分依赖贝塔过程的实验结果及分析 ................. 47
5.1 图像去噪问题 ................................................. 47
5.1.1 问题描述 ................................................. 47
5.1.2 求解方法 ................................................. 48
第五章 变分依赖贝塔过程的实验结果及分析
5.1 图像去噪问题
5.1.1求解方法
本文使用第四章提出的 VDBP 伯努利过程,将噪声图像中的图像块作为一个样本。将 VDBP 模型与伯努利过程结合,使用 VDBP 贝叶斯稀疏模型。给出如下贝叶斯概率图模型:
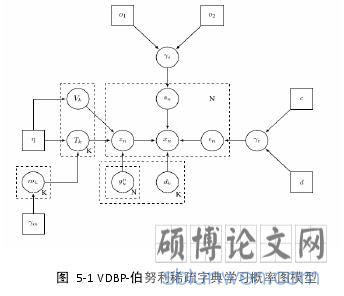
............................
总结及展望
6.1 本文总结
贝塔过程是一种在潜特征学习中常用的强有力的非参贝叶斯工具,其可以参数化伯努利过程,作为伯努利过程的先验。传统的贝塔过程假设数据顺序是可交换的,这会忽略时空或空间数据中固有的数据依赖关系。为了去除可交换性,依赖贝塔过程被提出,这些模型采用近似推理或者采样的方法推导模型。在此基础上主要研究了以下两个内容:
1. 将核贝塔过程用于对偶特征空间字典学习,使用依赖贝塔过程可以考虑数据样本携带的协变量信息。将该模型用于单幅图像超分辨率任务中,借助于引入到模型中的依赖信息,通过核函数对依赖信息进行建模。将其用于学习高、低分辨率特征空间中的字典和两个空间稀疏系数的关系映射矩阵。获得到高低分辨率字典和映射矩阵后,重构高分辨率图像。
2. 深度探索依赖贝塔过程模型,提出变分依赖贝塔过程,使用折棍构造的方法构建依赖贝塔过程。其优点是使用了折棍构造方法,可以对依赖贝塔过程进行精确的变分推理。将所提出的变分依赖贝塔过程与伯努利过程结合,并用于图像去噪以及图像修复两个经典任务中,给出实验结果作出相应的实验分析及总结。
参考文献(略)
