第 1 章 绪论
1.1 研究背景及意义
随着计算机网络技术日新月异的变化以及日益广泛的应用,计算机技术及应用系统在各行各业中发挥着越来越关键的作用。各领域对于计算机技术的依赖程度日益增强,在给我们工作生活带来方便和效率的同时,也意味着人们对系统软件的规模与复杂程度提出了更进一步的要求。而在系统规模日益庞大,功能日益复杂的情况下,如何保证系统软件的质量成为至关重要并无法规避的课题。例如在无人车自主控制系统[1]中,需要根据实时监测的环境信息,调动系统做出相应决策,包括:动态规划路径以实现到达目的地的最优路径、躲避静态和动态障碍物以及根据路况控制无人车速度。类似的无人机自主控制系统[2]要求根据传感器的态势感知,通过信息处理,任务重规划等操作,做出最优决策以适应感知的环境。这些系统都要求具有学习新需求并控制系统调整自身的行为以适应环境变化的能力,传统的软件系统往往考虑采集系统运行时尽可能多的预期环境情形,并依据经验给出相应的决策,最大程度上满足确定的需求。然而这种传统的软件系统无法涵盖所有的环境情形,并且难以动态地改变自身的行为以适应环境的变化。为了解决这一问题,人们尝试在传统的软件系统中嵌入一些智能组件,如神经网络,模糊规则等,组成了智能软件系统。
目前,智能软件系统被广泛的运用到各个领域,如移动机器人的避障与路径规划[3?4]、 无人机的自主智能和多机协同[5]、智能制造系统[6]等。智能软件系统具有学习新需求并控制系统适应环境变化这一性质,这种自适应性控制系统连续自动地监测被控对象的动态行为,将其与期望的输出进行比较,并利用这种差异来改变可调的系统参数或产生行为信号,使得无论系统环境如何变化都能给出相对最合适的行为。但同时智能软件系统中存在更多的不确定因素,如需求不确定、结构不确定等,这种不确定因素往往使系统的可靠性遭到了威胁,进而使保证系统质量面临更艰巨的挑战。因此,当一个智能软件系统被提出时,对其进行模型检查或验证以保证其质量是不可或缺的。
............................
1.2 国内外研究现状
模型验证通过搜索系统所有的可达状态检查给定模型和属性规范之间的一致性,它被广泛用于验证硬件和软件系统以确保所需的性能,是保证软件系统质量的重要手段[16]。构建智能系统时通常会依赖一些采集数据或者是经验数据,但这些数据本身的质量并不明确,这往往会影响整个系统的属性。以下,我们从智能软件系统的模型检查、验证以及智能模型中缺陷数据检测两方面简单地介绍相关的工作。
模型验证通过搜索系统所有的可达状态检查给定模型和属性规范之间的一致性,它被广泛用于验证硬件和软件系统以确保所需的性能,是保证软件系统质量的重要手段[16]。构建智能系统时通常会依赖一些采集数据或者是经验数据,但这些数据本身的质量并不明确,这往往会影响整个系统的属性。以下,我们从智能软件系统的模型检查、验证以及智能模型中缺陷数据检测两方面简单地介绍相关的工作。
1.2.1 智能软件系统模型检查、验证的研究
目前对智能软件系统模型检查、验证的研究相对集中在使用形式化的方法,并尝试在系统运行时保证模型的一些关键性质。
Clarke 等人[17]研究了与环境相互作用的自治空间系统的形式化验证。首先,集成形式化验证方法与马尔可夫模型,控制流分析和定理证明以开发新的工具来验证与控制流、通信协议和资源使用有关的属性。其次,利用混合概率模型的形式化验证技术分析与环境交互的系统。
Fisher 和 Wooldridge[18]提出使用时态置信逻辑对分布式人工智能(DAI)系统进行形式化规范与验证。首先提出了分布式人工智能系统的编程语言:并发元,用以对该系统进行建模,然后用时态置信逻辑语言来定义和验证并发元系统的属性。
为了自适应软件系统在软件生命周期实现持续保证,Cheng 等人[19]探讨了一种运行时保证技术:运行时模型(MAT)的使用,以保障自适应软件系统。
Weyns 等人[20]对自适应系统中的形式化方法进行了系统评价并得出一些结论:模型检查和定理证明关注有限,有一些重要自适应问题,如安全和可扩展性,很难被考虑。
................................
第 2 章 预备知识
3.1 基于自适应 Petri 网的建模...................13目前对智能软件系统模型检查、验证的研究相对集中在使用形式化的方法,并尝试在系统运行时保证模型的一些关键性质。
Clarke 等人[17]研究了与环境相互作用的自治空间系统的形式化验证。首先,集成形式化验证方法与马尔可夫模型,控制流分析和定理证明以开发新的工具来验证与控制流、通信协议和资源使用有关的属性。其次,利用混合概率模型的形式化验证技术分析与环境交互的系统。
Fisher 和 Wooldridge[18]提出使用时态置信逻辑对分布式人工智能(DAI)系统进行形式化规范与验证。首先提出了分布式人工智能系统的编程语言:并发元,用以对该系统进行建模,然后用时态置信逻辑语言来定义和验证并发元系统的属性。
为了自适应软件系统在软件生命周期实现持续保证,Cheng 等人[19]探讨了一种运行时保证技术:运行时模型(MAT)的使用,以保障自适应软件系统。
Weyns 等人[20]对自适应系统中的形式化方法进行了系统评价并得出一些结论:模型检查和定理证明关注有限,有一些重要自适应问题,如安全和可扩展性,很难被考虑。
................................
第 2 章 预备知识
2.1 Petri 网
1962年,Petri 博士发表了一篇博士论文,其中首次提出了 Petri 网的概念[32]。作为一种图形化的建模语言,Petri 网与其他图形,例如流程图、框图相似,可以被当作一种可视化通信平台。除此之外,系统中的一些复杂活动,如动态或并发过程也可以通过网络中的标识来模拟;另一方面,Petri 网能够发挥其强大的数学化建模功能,通过建立一些类似状态方程等数学模型分析系统的行为。基于以上两点,Petri 网是一种可以模拟系统并具有强大系统分析能力的工具。在研究类似并发、异步、分布式、并行以及存在不确定性因素的复杂系统中,Petri 网都发挥着十分重大的作用。

在 Petri 网中,不同元素需要用固有的图形表示,例如空心圆用来表示离散库所;竖直线表示变迁;用实心点来表示标识,通常实心点也可以用数字代替;有向弧用来连接库所和变迁。
Petri 网在模拟系统时,通常以库所代表系统的状态,以标识表示当前库所中含有的资源,以变迁代表系统的行为。一旦系统行为被触发,一定伴随着某些库所中标识的改变,相应的系统状态也会发生改变;同样的,系统行为的发生也受到系统状态即当前库所中标识分布的限制。正是靠着这种变迁的触发以及库所之间标识的流动,Petri 网才可以对系统复杂的动态运行过程进行模拟。
............................
1962年,Petri 博士发表了一篇博士论文,其中首次提出了 Petri 网的概念[32]。作为一种图形化的建模语言,Petri 网与其他图形,例如流程图、框图相似,可以被当作一种可视化通信平台。除此之外,系统中的一些复杂活动,如动态或并发过程也可以通过网络中的标识来模拟;另一方面,Petri 网能够发挥其强大的数学化建模功能,通过建立一些类似状态方程等数学模型分析系统的行为。基于以上两点,Petri 网是一种可以模拟系统并具有强大系统分析能力的工具。在研究类似并发、异步、分布式、并行以及存在不确定性因素的复杂系统中,Petri 网都发挥着十分重大的作用。

在 Petri 网中,不同元素需要用固有的图形表示,例如空心圆用来表示离散库所;竖直线表示变迁;用实心点来表示标识,通常实心点也可以用数字代替;有向弧用来连接库所和变迁。
Petri 网在模拟系统时,通常以库所代表系统的状态,以标识表示当前库所中含有的资源,以变迁代表系统的行为。一旦系统行为被触发,一定伴随着某些库所中标识的改变,相应的系统状态也会发生改变;同样的,系统行为的发生也受到系统状态即当前库所中标识分布的限制。正是靠着这种变迁的触发以及库所之间标识的流动,Petri 网才可以对系统复杂的动态运行过程进行模拟。
............................
2.2 神经网络
神经网络起源于上世纪五、六十年代,是一种仿照生物中枢神经系统的结构和功能建立的计算模型[34],可用于研究近似逼近非线性函数。它的一个重要性质是具有从样本数据中学习知识的能力:神经网络利用学习过程(算法)从其环境中获取知识,同时神经元间的连接强度 —— 权重,用来存储学习到的信息。神经网络这种强大的学习能力使得该技术在学术界和工业界都受到了高度的关注,并且广泛地应用到各个领域,如系统建模、自动控制等。
神经网络起源于上世纪五、六十年代,是一种仿照生物中枢神经系统的结构和功能建立的计算模型[34],可用于研究近似逼近非线性函数。它的一个重要性质是具有从样本数据中学习知识的能力:神经网络利用学习过程(算法)从其环境中获取知识,同时神经元间的连接强度 —— 权重,用来存储学习到的信息。神经网络这种强大的学习能力使得该技术在学术界和工业界都受到了高度的关注,并且广泛地应用到各个领域,如系统建模、自动控制等。
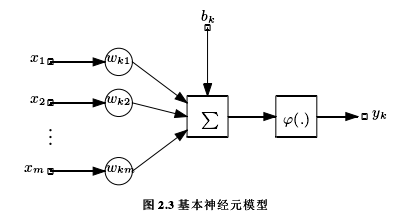
神经网络由简单的自适应处理单元(神经元)组成,神经元之间相互连接,形成一个大型的网络。作为神经网络的基本信息处理单元,神经元模型由三个(或四个)基本元素组成,其中包括:突触权重、加法器、激活函数,有时还存在一个外部施加的偏置项。
...........................
3 智智能软件系统的建模与验证...................13

...........................
3 智智能软件系统的建模与验证...................13
3.1.1 确定性需求建立 Petri 网...................13
3.1.2 样本数据训练神经网络...................13
4 定定位缺陷数据....................26
4.1 由属性定位缺陷部分....................26
4.2 由缺陷部分定位模糊规则....................26
5 实实例分析.........................30
5.1 引例 .........................30
5.2 智能制造系统的自适应 Petri 网模型.........................30
第 5 章 实例分析
5.1 引例
一个制造企业的供应链模型可以看作是订单、产品设计、制造、业务等不同过程中多个不同参与者的一个合作过程。生产经营的复杂性决定了供应商的选择是一种动态实时的决策过程。制造企业间流程具有与离散生产过程相结合、管理规模扩大、业务扩展灵活、对市场需求反应迅速、智能化等特点。
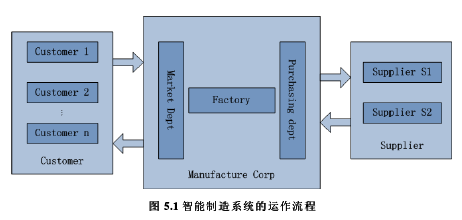
为了方便分析,本文精简了原模型的某些部分。智能制造系统的运作流程如图5.1 所示,客户下订单后,市场部负责整理并分析这些订单信息,制定生产计划,生产部和采购部根据下发的生产计划相互配合完成工作,其中生产部主要负责与合作的工厂进行任务交接(本文只考虑有指定工厂的情况),采购部主要负责选择合适的供应商。
.........................
第 6 章 总结与展望
目前,智能软件系统被广泛的运用到各个领域,但面临的一个关键挑战是如何保证系统自身的质量。国内外研究者对此展开了诸多研究,但是在保证模型质量的研究上缺乏对数据质量的关注。本文通过智能软件系统的模型验证技术逆向追踪系统中智能模型的缺陷数据,主要完成了以下几方面的工作:
(1)构建自适应 Petri 网模型以描述整个智能软件系统。自适应 Petri 网是常规Petri 网的扩展,其中包括两部分:一部分是一般的 Petri 网模型,用来对智能软件系统中的传统组件—— 确定的软件需求建模;另一部分是神经网络模型,在自适应 Petri网中,以自适应变迁表示,用来对智能软件系统中的智能组件——只有输入输出,无法描述确定行为的部分建模。
(2)对智能软件系统进行模型验证。自适应 Petri 网虽然能够对智能软件系统建模,但无法通过传统的模型验证工具直接分析。通过各种模型转换规则,其中包括:从神经网络中提取模糊规则、模糊规则与 Petri 网之间的转换等将原自适应 Petri 网模型转换成为可以通过模型验证工具分析的模型。最后通过工具 Ke Ymaer 进行了属性的验证。
(3)提出了一种定位智能软件系统中智能模型的缺陷数据的方法。整个定位缺陷数据的过程是一个逆向追踪的过程:首先由工具 Ke Ymaera 提供的属性违反报告定位到混合模型的缺陷部分,然后由模型的缺陷部分定位到具体的模糊规则,最后利用提出的两阶段逆映射方法定位到缺陷的数据。
参考文献(略)
