第一章 绪论
1.1 计算机模拟概述
自 1949 年世界上第一台计算机诞生以来,计算机经历了从电子管、晶体管、集成电路到超大规模集成电路的时代。计算机模拟技术也取得了高速的发展,近年来被广泛应用于材料学、物理学、生命科学等领域。计算机模拟技术弥补了传统实验和理论的一些缺陷,并且与实验和理论形成了三足鼎立之势[12]。一方面,计算机模拟不仅能够对实验中无法观测的现象进行定性的描述,直观的获得微观、介观形貌,而且可以定量的计算材料的物理化学性质,由此为材料的设计提供可行的路线;另一方面,计算机模拟还可以对理论进行验证和补充,对理论提出的模型进行优化。计算机模拟存在安全性高、可行性强、效率高、无污染等优点,这些优点大大节约了人力、物力,缩短了材料的研发周期,对材料领域的发展有着极为重要的意义。伴随着近几十年来计算机硬件、软件和算法的飞速发展,计算机的计算能力显著提高,计算机模拟成为人类科学探索的第三类方式[13]。
计算机组装论文参考
1.2 基于 GPU 高性能计算的分子动力学模拟
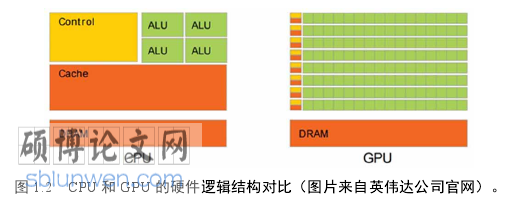
图形处理器(Graphics processing unit),简称为 GPU,与中央处理器一样,都是电脑的核心部分。下图是两种处理器的内部结构,其中 ALU 是算术逻辑单元,Cache 是 CPU 内部缓存,Control 是控制器,DRAM 是内存。GPU 省去了Cache,保留了更多的计算单元,更加擅长对数据进行简单重复的操作。与 CPU相比,GPU 有很多优点。第一点,GPU 可以提供多核计算的基础结构,且较多的核心数可以支持大量的并行计算,而并行计算相对于串行计算来说,可以同时执行多个命令,增加计算速度,求解更复杂的问题;第二点,GPU 拥有更高的访存速度;第三点,GPU 拥有更高的浮点计算能力。这些优点使得 GPU 成为了一种应用于计算领域的重要工具。
计算机组装论文怎么写
GPU 要在计算领域得到广泛的应用,其关键点还是在于并行化算法设计。2007 年 NVIDIA 公司推出了一种运算平台 CUDA(Compute Unified Device Architecture),通过 CUDA,GPU 可以并行处理大量复杂的计算。科研人员可以使用 C 语言结合 CUDA C 进行并行程序的编写,编写后的并行程序在CUDATM处理器上得到高效率的执行。经过多年的发展,CUDA C 已经开发了多种支持 C 语言的调用数学库函数,非常有力的支持了 GPU 的并行加速。
对于计算机模拟来说,精度高、计算速度快、运行环境稳定的 GPU 越来越有吸引力。目前很多计算机模拟程序都开发了 GPU 版本,比如 HOOMD、GALAMOST、GROMACS、LAMMPS 等。
.........................
第二章 理论基础
2.1 分子动力学模拟
分子动力学模拟方法是一种在原子、分子水平上求解多体问题的模拟方法。该方法中粒子的运动遵循经典的牛顿运动方程。通过模拟体系随着时间的演化,获取粒子的位置、速度等信息,利用统计力学的方法获得体系的结构和动力学信息。模拟粒子运动时,我们设定一个时间步长 t,将连续的时间分隔为间隔为t 的时间点,通过计算每个时间点上粒子的受力,从而得到下一个时间点粒子的位置和速度信息。
在分子动力学模拟中,计算时通常选取数目为 N 的分子,将其置于边长为L 的立方体盒子中。为了保证模拟过程的密度恒定,一般采用周期性边界条件(Periodic Boundary Condition)。以二维的体系为例,如图 2.2 所示。图中正中间的盒子是中央盒子,周围的镜像系统与中间的模拟盒子具有相同的运动和排列。模拟中,当体系中随机的粒子移动到盒子外面,必然会有对应的粒子从其相对的方向进入,这种方式最终保证了体系的密度恒定。对于液体或者溶液这种非周期性的体系,由于孤立团簇导致的边界问题被周期性边界条件引起的问题取代,周期性边界条件就会产生误差,通过对不同尺寸模拟体系进行比较可以估计这种误差。
最近几年,很多科研组致力于研究 TNP 体系的自组装。实验上,得益于合成技术的领先,Cheng 领导科研组开展了很多相关工作。他们通过点击化学的方法,将多面体半倍硅氧烷(POSS)或者富勒烯(AC60)与聚合物链连接,合成了具有精准形状的巨型分子[8][41]-[46]。他们发现随着羧酸电离程度的增加,具有亲水头部和疏水尾部的 APOSS-PS 分子在溶液中的自组装形貌会从囊泡到蠕虫状,进一步向着球状演变。由此提出了一种控制自组装形貌的方法[8]。在胶束形态的演变过程中,APOSS-APOSS 之间的相互作用有着很重要的影响。与传统嵌段共聚物相比,APOSS-PS 体系中 PS 链在胶束核中更加的伸展。
.......................
2.2 耗散粒子动力学的积分算法
在分子动力学中,积分算法的发展已经较为完善。然而在耗散粒子动力学中,积分算法目前还存在两方面的问题:一是由于耗散粒子动力学中存在随机力,使得体系的时间可逆性消失;二是耗散力与作用的 DPD 珠子的速度成正比,而且会影响 DPD 珠子的速度,最终给 DPD 的积分算法带来了困难,而且会引起物理量计算上的一些偏差。DPD 的积分算法主要包括:DPD-velocity-Verlet(DPD-VV)算法,GW-VV 方法,S1 方法,Lowe-Andersen 等方法。在本文中,主要运用 DPD-VV 算法,我们对 DPD-VV 算法进行简单的介绍。DPD-VV 算法属于经典的 verlet 算法,该算法优点是不引入任何调节参数,且需要提供信息较少,程序编写简单,计算速度快;缺点是计算稳定性较差,精确度不够。
为了把真实体系中原子分子的信息映射到 DPD 模拟方法中,采用将 DPD与 Flory-Huggins 平均场理论结合的方法,让模拟体系更接近于真实体系,模拟结果更加能反映聚合物的真实性质。通过将 DPD 中的保守力相互作用参数与Flory-Huggins 中的χ参数结合起来,可以将原子分子的信息映射到 DPD 中,实现对真实聚合物体系热力学性质和动力学性质的计算。
通过化学键将形状和体积固定的纳米粒子头部和组成不同的柔性聚合物尾部连接起来,可以组成各种不同的 TNP。一种尺寸更大的 TNP 也称为巨型分子,这类巨型分子与小分子有类似的结构特征,可以很好的保证其分子结构和对称性,但是尺寸更大。这类巨型分子在溶液中,由于纳米粒子和聚合物熵和焓之间的竞争,可以自组装形成一系列的胶束、囊泡形貌,而且由于巨型分子的纳米粒子头部具有一定的形状和体积,其自组装过程存在着位阻效应,TNP 体系可以得到更多形貌丰富的组装结构。
............................
第三章 接枝纳米立方体在溶液中的自组装 ......................................14
3.1 引言 ........................................14
3.2 模拟方法 ...........................................16
3.3 模型构建 ..................................16
第四章 可调控形状的接枝纳米粒子在溶液中的自组装 ..................23
4.1 引言 ......................................23
4.2 模拟方法 ......................................24
4.3 模型构建 ....................................24
第五章 总结 ............................29
第四章 可调控形状的接枝纳米粒子在溶液中的自组装
4.1 引言
随着合成技术的飞速发展,许多纳米粒子的形状和大小可以响应外部刺激以及分子输入而改变[11]。Yoo 和 Mitragotri[67]合成了聚乳酸-共聚糖内酯(lactide-co-glycolide)(PLGA)粒子,这种粒子的形状可以由温度、pH 值和化学添加剂来控制。PLGA 粒子的形状转变过程可以在几分钟到几天内被精准控制。Gang 等人[68]将十二烷基硫醇配体链接枝到立方体钯纳米颗粒上,这些配体链在纳米颗粒表面形成一个软壳。通过蒸发溶剂,粒子可以实现形状的改变,并且粒子的晶格排列会随着粒子的形状从立方体过渡到球状变化而发生变化。一些模拟同样也关注形状可以改变的粒子的有序排列情况。Ni 等人[69]运用蒙特卡罗中自由能分析的方法,对形状可以从立方体经球体,最后向八面体转变的胶体硬纳米粒子的排列进行了模拟,构建了纳米粒子排列变化的相图。他们发现硬胶体粒子在近似球时呈面心立方排列,形状接近八面体时粒子排列呈稳定的体心立方。不同形状的粒子对结构排列的稳定性有重要影响。Glotzer 等人[70][71]基于纳米粒子模型,通过几何驱动自组装的方法获得了很多堆积结构。她们模拟了可以动态改变形状的纳米粒子的自组装,研究了不同的形状改变过程中体系有序-有序的转变,同时证实了不同形状纳米粒子的有序排列可以通过不同的形状转变过程获得。她们的研究表明了怎么通过一个固定的初始结构,经历不同的粒子重构路线,获得目标的排列结构。
在第三章中,我们研究了纳米立方体的形状和溶剂条件以及接枝链长对 TNP 体系自组装的影响。上述的纳米粒子表面并没有被任何的配体修饰,纳米立方体可以完全的表现出自己的形状。然而,在大多数实验中,纳米粒子通常是被各种配体链所修饰,比如 Gang 等人[68]将十二烷基硫醇配体链接枝到立方钯纳米颗粒上,通过控制配体链形成的软壳达到控制纳米粒子形状的目的。接枝配体链的体系[72][73]由于其配体链形成的软壳构建了不同的几何形状,而且配体链间存在相互作用,所以其自组装行为与纯几何体相比差异较大。同时接枝配体链体系的几何形状和壳的性质也成为了一种新的调控自组装的参数。
...............................
第五章 总结
本文运用耗散粒子动力学方法(DPD)探究了可调控形状的接枝纳米粒子在稀溶液中的自组装行为。在纳米粒子是刚性纳米立方体的情况下,我们通过改变刚性的纳米立方体和溶剂间的相互作用以及接枝链长,获得了一系列聚集结构。当纳米立方体是亲水性的时候,具有疏水性尾部的接枝纳米立方体自组装形成以接枝链为核,纳米立方体为壳的经典胶束结构,纳米立方体均匀的分布在胶束的表面。随着纳米立方体越来越疏水,纳米立方体开始聚集,模拟得到了一些基于纳米立方体形状排列的有序聚集体,纳米立方体的几何形状驱动了这些聚集体的形成。
在大量实验中,纳米粒子表面通常被一些接枝链修饰,通过控制接枝密度来控制接枝链形成的软壳。我们建立了一个刚性纳米立方体被软壳包围的模型,用软壳来模拟接枝链以及溶剂在接枝链附近的吸附效果。调节软壳间以及软壳和溶剂间的相互作用相当于调节接枝密度。从接枝纳米粒子聚集的角度来看,在纳米立方体表面修饰一些亲水的接枝链(在软壳间使用小的相互作用参数)可以让接枝纳米粒子体系马上聚集成一些小胶束。增加软壳间的相互作用,模拟了大的接枝密度下链的重叠导致了位阻增加的过程,此时纳米粒子从立方体向球体转变。在这种情况下,聚集体开始粘黏在一起,纳米粒子在胶束表面的排列也从四方(立方体)变为六方(球体)。
我们的模拟结果描述了一种对接枝纳米粒子(TNP)自组装体系新的设计可能性,同时也证明了纳米粒子形状对接枝纳米粒子体系排列和自组装结构的影响。对下一代新材料的设计有重要意义。
参考文献(略)
