本文是一篇经济论文,本篇文章在研究金融时间序列收益率之间的相关性时,虽然用到了大量的静态 Copula 函数以及动态 Copula 函数,但如今我们处在一个大数据时代,现阶段学者研究出的 Copula 函数已经不能满足大量类型复杂、结构多变的数据,因此研究出新的 Copula 函数是广大学者可以钻研的一个方向。
第 1 章 引言
1.1 背景介绍
近年来,随着经济的快速发展,各金融资产之间的联系变得更加密切,其结构也变得日益复杂、多样。金融危机的频繁发生也使得国内外的学者更加关注金融资产间的相依关系。以往,相关学者在探究金融时间收益率序列分布时会假设其服从正态分布,不过如今有大量的试验证明,正态性假设并不符合事实,金融时间序列通常具有偏斜、尖峰、厚尾的特征。其次,各金融资产之间的相关性也并不是线性的,因此两个金融资产之间复杂的相关性不能简单地用相关系数度量。再者,金融资产之间的相关关系会随着时间的变化而变化。而 Copula 函数刚好解决了这些问题,Copula 函数的几点优势如下:第一,使用 Copula 模型研究各金融资产间的相关关系时,不需要假设各个资产收益率序列的分布函数类型,克服了传统模型中需要求解两个序列联合分布函数的密度函数的不足。第二,Copula 函数能够度量金融时间序列之间的非线性关系。第三,时变 Copula 模型可以研究随着时间的变化而变化的金融时间序列。
...........................
1.2 文献综述
1959 年,Sklar 第一次提出 Copula 的概念,研究发现一个联合分布函数能够拆分成构成它的各随机变量的边缘分布和一个连接函数,即 Copula 函数。这种连接函数能够很好地描述不同变量之间的相关关系,一个 Copula 函数和多个随机变量的分布函数可以组成一个多维联合分布函数[1]。Copula 函数在最初时期由于各种条件的限制,并没有得到广大学者们的重视,直到将近 40 年后的 1998年,Nelsen 撰写了《An introduction to copula》一书,主要介绍了 Copula 函数的性质和意义,并阐述了 Copula 函数的数学构造基础[2]。1999 年,Embrechts 将Copula 模型引入到金融领域,使用 Copula 函数来衡量各个金融收益率序列之间的相关性[3]。2001 年,Patton 研究了 Copula 函数在时间序列建模中的应用,提出可以把 GARCH 模型与 Copula 模型结合起来,构造 Copula-GARCH 模型来研究时间序列[4]。2006 年 Jondeau 和 Rockinger 用 Copula-GARCH 模型对金融指数间的相关性进行了研究,最终得出 t 分布的 Copula 函数能更好的刻画金融资产间的相关性[5]。随后,Roch 与 Alcgre 用 ARMA-GARCH 模型拟合资产的边缘分布,并结合 Copula 模型对西班牙股市间的相依关系进行研究[6]。2017 年,Mokni和 Mansouri 根据国际上主要股票市场间的关系,构建 GARCH-t-Copula 模型并进行市场风险估计[7]。Patton 是最早研究动态 Copula 模型的学者之一,他研究了日元与美元、英镑与美元汇率之间的关联性,研究结果显示在欧元体系推出前后,这两种汇率之间的相关性发生了巨大变化。基于此,Patton 提出了可以使用ARMA(1,10)模型来拟合动态 Copula 函数的相关参数[8-12]。Andersen 和 Bauwens也一致认为条件相关性会随着时间变化而变化,因此需要在研究过程中引入时变Copula 函数族[13]。Garcia 和 Tsafack 为了使用 Copula 函数探究债市与股市之间的关联性,他们研究了两个国家的股票和债券四个资产的组合,开创了研究多个金融资产投资组合的先河[14]。Taylor 和 Bartram 使用时变的 Copula 模型来拟合欧洲股票市场的数据,得到了很好的结果[15]。
国内对 Copula 函数的研究相比国外起步较晚,但最近几年发展较快。2002年,张尧庭在研究相关性指标时第一次使用 Copula 函数,并阐述了 Copula 函数的定义、性质[16]。2004 年,韦艳华和张世英构建 Copula-GARCH 模型研究了上海证券市场几个板块间的相依关系[17]。缪柏其和叶五一等将 Copula 理论应用到高频连涨连跌收益率的相依关系研究并进行了 CVaR 分析[18]。随后,刘喜波等利用 Copula 函数从定量角度分析了沪、深股市日收益率的相关性,得出在平方欧式距离标准下,沪、深股市的日收益率序列用 t-Copula 拟合最好[19]。
..................................
第 2 章基于时变 Copula 模型的国内股票市场尾部相关性的研究
2.1实证分析
2.2.1 数据的选取以及预处理
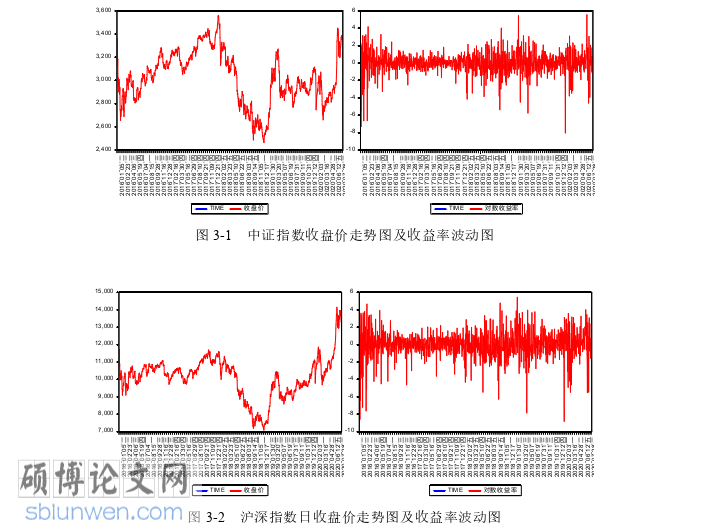
本章选取中证指数(IC8888)和沪深指数(IF8888)从 2016 年 1 月 4 日至2020 年 8 月 13 日的日收盘价作为原始数据,共 1124 组观测值,数据来源于同花顺软件数据库。tP 表示日收盘价,以 1100logtttR PP表示收益率序列,转化为收益率之后为 1123 组数据。
图 3-1 和图 3-2 反映了中证指数和沪深指数自 2016 年以来的日收盘价走势以及收益率的波动情况。中证指数和沪深指数在 2016 年相对稳定且在 2017 年有上升趋势,在 2018 年年初骤降,年中一直处于较为低靡状态,年末大幅度上升,之后基本趋于稳定,但在 2020 年 6 月又出现大幅度上升。总体上的波动呈现出一定的同步性。
经济论文怎么写
对中证指数和沪深指数的收益率序列进行统计分析,图 3-3 和图 3-4 为样本收益率的频率直方图,从直方图中大致可以看出中证指数和沪深指数两个日收益率序列的峰值都很高,而且呈现出有偏和厚尾的性质。表 3-1 为中证指数和沪深指数的描述性统计结果,偏度-1.037<0、-0.904<0 且峰度 10.265>3、7.796>3,可得到两个收益率序列呈现尖峰和左偏的分布特性。
.........................
2.2ARMA 模型的选择
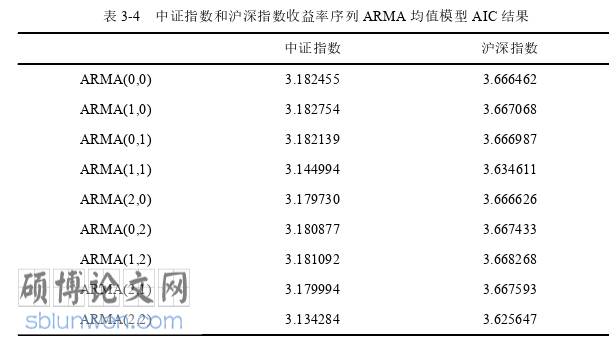
根据 AIC 值最小原则,中证指数和沪深指数最终都选择了 ARMA(2,2)模型。
经济论文怎么写
对中证指数和沪深指数的收益率序列 ARMA(2,2)均值过程做 ARCH-LM 检验,得到中证指数和沪深指数的 p 值分别为 0.0432<0.1 和 0.0985<0.1,拒绝残差不具备相关性的原假设,因此得到中证指数和沪深指数去均值化的收益率序列具有 ARCH 效应。
........................
第 3 章 基于时变 Copula 模型的国内股票市场尾部相关性的研究.................... 13
3.1 ARMA-GARCH-t-Copula 模型构建..............................13
3.2 实证分析.........................................13
第 4 章 基于时变 SJC-Copula 模型的国内外股票市场尾部相依关系的研究.....24
4.1 ARMA-GARCH-t-Copula 模型.........................................24
4.2 ARMA-EGARCH-t-Copula 模型............................. 24
第 5 章 结论与展望..............................35
5.1 结论...................................35
5.2 展望....................................35
第 4 章 基于时变 SJC-Copula 模型的国内外股票市场尾部相依关系的研究
4.3 实证分析
4.3.1 数据的选取以及预处理
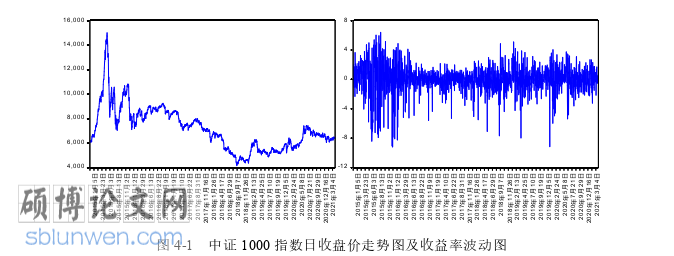
选择中证 1000 指数(CSI1000I)、香港恒生指数(HSI)、美国标准普尔500 指数(SPX)和日经 225 指数(N225)从 2015 年 1 月 6 日到 2021 年 4 月 30日的日收盘价作为原始数据,tP 表示日收盘价,以 1100logtttR PP表示收益率序列,剔除缺失日期的数据,得到 1380 组收益率序列。数据源于英为财情。
经济论文参考
以中证 1000 指数作为我国股票市场的代表,图 4-1 反映了中证指数自 2015年以来的日收盘价走势以及收益率的波动情况,在 2015 年我国牛熊市转换期间波动较大,收盘价骤升以后出现断崖式下跌,2016 年相对稳定且在 2017 年有上升趋势,在 2018 年年初骤降,年中一直处于较为低靡状态,年末大幅度上升,之后基本趋于稳定,2020 年年初新冠疫情爆发期间出现小幅度动荡,从 6 月开始一路高涨,之后趋于稳定。
.............................
第 5 章 结论与展望
5.1 结论
经济的快速发展使金融资产间结构呈现出多样化,而 Copula 函数的出现为研究金融资产间相关性提供了及其重要的参考价值。文章先介绍相关理论知识,再将 Copula 模型运用到了资产间相关性的研究应用中,其主要研究内容如下:
国内股票市场:基于时变 Copula 函数,构建 ARMA-GARCH-t-Copula 模型研究中证指数与沪深指数的日收益率序列的尾部相依关系,得到 t -Copula 函数在静态 Copula 模型中拟合效果最好,中证指数和沪深指数之间不仅存在着较强的相关性,且两者间存在着正向的尾部关系,会出现同时增长或者同时下跌的情况。在动态 Copula 中对收益率序列相依关系刻画最佳的是 Rotated Gumbel Copula函数,且要优于在静态 Copula 函数拟合效果最好的 t Copula 模型。无论是静态Copula 还是动态 Copula,中证指数与沪深指数的下尾相关性要强于上尾相关性。
国内外股票市场:基于时变 SJC-Copula 函数,构建 ARMA-GARCH-t-Copula模型和 ARMA-EGARCH-t-Copula 模型研究中证 1000 指数与香港恒生指数、中证 1000 指数与美国标准普尔指数、中证 1000 指数与日经 255 指数和香港恒生指数与美国标准普尔指数的尾部时变相依关系。得到中国大陆股票市场和香港股票市场的下尾相关性要大于上尾相关性,且上尾相关系数随着时间的变化波动较大;中国大陆股票市场与美国、日本股票市场的上尾相关系数随着时间变化的波动性要大于下尾相关系数;香港股票市场与美国股票市场的尾部相依性要大于中国大陆股票市场与美国股票市场的尾部相依性。
参考文献(略)
