
第 1 章 绪论
1.1 课题研究背景
1.1.1 无线传感网络简介
随着传感器技术、嵌入式计算技术和分布式通信技术的飞速发展[1,2],无线传感器网络(Wireless Sensor Networks, WSNs)的应用领域得到了拓展,逐渐成为现今的研究热点。WSNs 是由部署在监测区域内大量的低成本微型传感器通过自组织的方式形成的多跳无线通信网络[3],它可以感知、采集各种环境和监测对象的信息,并以无线通信的方式将消息发送至观察者,从而实现物理世界、信息化世界以及人类社会的三元连通。
WSNs 中节点部署便捷,网络不需要定期维护,感知消息的传递不依赖于基站。其中微型传感器技术、无线通信技术、自组织性、高容错性和强隐蔽性等技术优势使得 WSNs 在国防、智能交通、生态环境监测、紧急预警等领域应用广泛,但是 WSNs 也具有明显的缺点[5],例如电源能量有限、通信能力有限、节点计算能力有限等[6]。因此研究者通常从能量管理、拓扑管理、网络安全等方面对 WSNs 进行研究。
WSNs 中,传感器节点携带能量有限的干电池供电,能量资源受限使得降低节点能耗,延长网络运行时间成为了 WSNs 一个重要研究方向。目前,无线传感网络中感知节点可通过配备充电技术延长节点的寿命,进而提升网络的运行时间。Haifeng Lin [7]等人对节点剩余能量和数据收集率建立数学模型,将可充电无线传感网络中节点数据采集率与节点剩余能量的关系转化为优化问题,引入拉格朗日乘子和次梯度算法,采用拓扑控制方案增强节点间通信能力,实验表明,该算法可以提升网络数据转发效率。在节点通信过程中,也可以通过优化上层协议,降低节点能耗,最大化无线传感器网络生命周期[8-10]。与无线传感网络不同,机会传感网络存在多个互不连通的区域,网络中链路的建立依赖于移动节点,节点间链路的建立具有机会性,这种依赖于移动节点与区域和 Sink节点的机会性连接达到消息传递的目的是两种网络的本质不同。
.................................
1.2 论文研究意义
OSNs 信息传输并不要求整网的全连通[14],即不需要源节点和目标节点之间长时间存在端到端路径,因此非常适用于实际环境下的组网要求,在野生生物追踪、生态环境监测网络、无线车载自组织网络、以及偏远地区网络传输等网络易分裂的恶劣环境有着广泛的应用前景。网络连通性是衡量网络性能的一项重要指标,通过分析各种网络的连通性,可以帮助我们设计路由协议和数据分流策略。此外,通过连通性分析得到的有关网络连通性度量参数还可以帮助我们监视整个网络,分析网络各个节点的运行状况以及网络运行环境的变化情况。因此,研究网络连通性可以为优化网络结构,提高网络运行质量提供理论依据。
区别于静态网络和无线传感网络,机会传感网络的消息传递主要依赖于Ferry 节点“存储-携带-转发”的能力,因此两者的拓扑变化有明显的区别,前者的网络拓扑较为稳定,网络中的通信链路较为持久,因此可采用图论知识获得节点度、节点介数以及网络直径等连通性参数,用这些参数来反映网络的连通性能。OSNs 中,节点的移动导致感知节点与 Ferry 节点、Ferry 与 Ferry 节点、Ferry 节点与 Sink 节点的链路处于不稳定的状态,这使得 OSNs 网络连通性会随着时间动态变化,因此采用何种指标度量网络连通性的变化情况,刻画节点链路建立过程,是描述机会传感网络连通性的首要问题。本文结合时空图理论,从消息层面和网络的拓扑结构层面出发,构建了连通性模型表征机会传感网络连通性,通过实验验证了模型的合理性和适用性。本课题来源于国家自然科学基金,机会传感网络连通性监视方法研究(N0.61262020)。本文对该项目中“机会传感网络连通性模型的建立”部分进行了研究。
...........................
第 2 章 网络连通性研究
2.1 静态网络连通性研究
静态 WSNs 中,节点在区域内指定位置采集消息,拓扑保持恒定,节点间链路的稳定性更强。因此常用节点的度、节点的介数以及网络直径等度量指标描述网络连通性,此外还可以通过静态图构建连通性模型描述网络的连通状况。
第 3 章 基于消息传输的网络连通性模型 ......................................10第 2 章 网络连通性研究
2.1 静态网络连通性研究
静态 WSNs 中,节点在区域内指定位置采集消息,拓扑保持恒定,节点间链路的稳定性更强。因此常用节点的度、节点的介数以及网络直径等度量指标描述网络连通性,此外还可以通过静态图构建连通性模型描述网络的连通状况。
文献[15]在保持网络连通情况下,给出了无线传感网络 k 连通和 3 连通公式,并分析了网络中边界节点对连通度的影响。文献[16]研究了不可靠链路下无线网络中连通度与传输时延的问题,基于渗流理论,建立静态和动态模型,根据节点间欧氏距离,获得连通性发生变化的临界节点密度。文献[17]通过 SPCCA算法找出 WSNs 中冗余节点并将冗余节点设置为休眠模式,唤醒 WSNs 中候选节点确保连通度和覆盖度达到要求,由仿真结果可知,SPCCA 算法可以增大静态无线传感网络活中有效节点数和网络运行时长。Z Khalid 等人[18]研究了 N 个节点在球面和球体的连通性,采用几何概率求出单个节点落在球体内的条件概率并计算出两种拓扑结构下节点度平均值、节点孤立率以及连通度上界。
由于静态网络布置规模较大,因此,如何控制网络中节点的能耗也是研究的领域之一。除连通性之外,许多文献结合能量和连通性作为目标进行研究。文献[19]提出了AAEECC算法,该算法首先建立了最小跳数连通图,接着提出了节点调度策略以达到期望的网络覆盖度,最后定义了容错连接维护算法解决了因调度引起的网络断开的问题并通过仿真实验验证了该算法的可行性。文献[20]在电磁波系统和磁感应系统下,研究了对影响地下无线传感网络的连通性能的参数和节点孤立概率建立模型,将仿真结果与模型结论对比分析,这为设计可靠的地下无线传感网络提供了理论依据。文献[21]提出一种感知数据采集协议,周期性的打开、关闭节点的无线通信模块减少节点能耗,通过定期维护中继节点与冗余节点以确保网络连通性,每个感知节点将其感知数据发送至最近的独立节点,独立节点通过中继节点发送至接收者,仿真结果表明,协议在满足覆盖率、包接受率、连通度的前提下延长了网络的生存时间。
..............................
..............................
2.2 动态网络连通性研究
当网络中存在动态节点时,其拓扑随时间变化而变化,所以静态网络的研究方法与指标不适用于动态网络连通性的研究。当网络拓扑呈动态变化时,该类网络连通性的研究可以从节点移动模型和路由协议出发,结合静态网络的连通性参数和网络的特点,综合考虑网络的连通性能。文献[25]无线传感网络由车载传感器和静态传感器组成,以网络全连通为基础,使用 K-均值法和 Kruskal算法寻找车载传感器数量的最小值,通过改变车载传感器数量、周期间隔以及车载传感器传输半径进行仿真实验,实验结果表明,与简单逼近法相比,使用K-均值法和 Kruskal 算法使用的车载传感器平均减少了 58.84%。文献[26]提出了基于环境学习的监测系统,将移动节点位置问题转化为最大化连通度和覆盖度问题,通过整数线性规划模型,确定移动节点的位置,此外还提出了三种启发式算法解决连通约束的网络覆盖度问题。Leonardo 等人[27]采用真实数据集,分析网络中移动节点对网络整体连通性和局部连通性的影响,仿真实验得到的分析结果为设计高效的 Ad-hoc 网络通信算法提供了理论依据。文献[28]采用欧氏距离生成树模型和 AVABC 算法提高网络的连通性和生存时间,仿真实验表明,基于欧式距离生成树的 AVABC 算法相比于其他算法,能有效解决移动节点部署问题,达到最小化移动节点移动距离和网络能耗的目的。文献[29]提出了一种新的自适应拓扑算法,根据该算法,网络中每一个节点按照整网连通情况优化其传输半径,通过仿真实验,所提出的拓扑控制算法与其他算法相比,既能减小端至端时延,又能降低网络能耗。文献[30]从移动自组织网络连通度和能耗方面出发,提出了 EBUM 演算模型,用于分析、评估、比较能量感知协议和算法,衡量网络中某些指标大小,如干扰和冲突的数量和损失程度。文献[31]采用时空层次图模型对代理节点进行分层,设计节点激活机制,以减少消息传输的能耗和定位的网络流量开销。在随机路点模型下,为了确保网络 2-连通,文献[32]构建网络节点密度与 2-连通数学模型,结果表明,当节点密度呈指数增长时,网络 2-连通的几率也随着增长,但存在阈值,此外还比较了 MHD 与 LRD两种优化准则的优劣性。在文献[33]总结了网络连接的相关文献,确定了影响移动自组织网络连通度的重要参数,例如电源故障、链路失效、关键节点以及节点失效等,面临的主要问题:链路预测、网络能耗以及连接效率与成本。
............................
当网络中存在动态节点时,其拓扑随时间变化而变化,所以静态网络的研究方法与指标不适用于动态网络连通性的研究。当网络拓扑呈动态变化时,该类网络连通性的研究可以从节点移动模型和路由协议出发,结合静态网络的连通性参数和网络的特点,综合考虑网络的连通性能。文献[25]无线传感网络由车载传感器和静态传感器组成,以网络全连通为基础,使用 K-均值法和 Kruskal算法寻找车载传感器数量的最小值,通过改变车载传感器数量、周期间隔以及车载传感器传输半径进行仿真实验,实验结果表明,与简单逼近法相比,使用K-均值法和 Kruskal 算法使用的车载传感器平均减少了 58.84%。文献[26]提出了基于环境学习的监测系统,将移动节点位置问题转化为最大化连通度和覆盖度问题,通过整数线性规划模型,确定移动节点的位置,此外还提出了三种启发式算法解决连通约束的网络覆盖度问题。Leonardo 等人[27]采用真实数据集,分析网络中移动节点对网络整体连通性和局部连通性的影响,仿真实验得到的分析结果为设计高效的 Ad-hoc 网络通信算法提供了理论依据。文献[28]采用欧氏距离生成树模型和 AVABC 算法提高网络的连通性和生存时间,仿真实验表明,基于欧式距离生成树的 AVABC 算法相比于其他算法,能有效解决移动节点部署问题,达到最小化移动节点移动距离和网络能耗的目的。文献[29]提出了一种新的自适应拓扑算法,根据该算法,网络中每一个节点按照整网连通情况优化其传输半径,通过仿真实验,所提出的拓扑控制算法与其他算法相比,既能减小端至端时延,又能降低网络能耗。文献[30]从移动自组织网络连通度和能耗方面出发,提出了 EBUM 演算模型,用于分析、评估、比较能量感知协议和算法,衡量网络中某些指标大小,如干扰和冲突的数量和损失程度。文献[31]采用时空层次图模型对代理节点进行分层,设计节点激活机制,以减少消息传输的能耗和定位的网络流量开销。在随机路点模型下,为了确保网络 2-连通,文献[32]构建网络节点密度与 2-连通数学模型,结果表明,当节点密度呈指数增长时,网络 2-连通的几率也随着增长,但存在阈值,此外还比较了 MHD 与 LRD两种优化准则的优劣性。在文献[33]总结了网络连接的相关文献,确定了影响移动自组织网络连通度的重要参数,例如电源故障、链路失效、关键节点以及节点失效等,面临的主要问题:链路预测、网络能耗以及连接效率与成本。
............................
3.1 多区域 OSNs 场景描述与分析 ............................10
3.2 时空图模型 .................................. 11
3.3 连通性建模 ................................12
第 4 章 基于节点度的整网连通性模型 .......................................27
4.1 问题分析 ...................................27
4.2 机会传感网络分层模型..............27
第 5 章 实验结果分析与评价 .....................................35
5.1 仿真实验设计与分析 .....................................35
5.1.1 Ferry 节点速度变化的网络连通度实验 ..........................35
5.1.2 Ferry 节点个数变化的网络连通度实验 ...............................38
第 5 章 实验结果分析与评价
5.1 仿真实验设计与分析
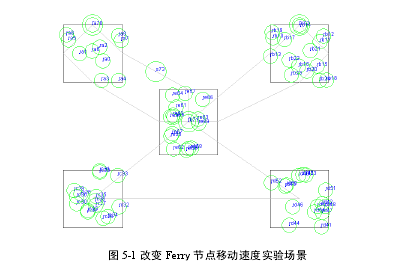
5.1.1 Ferry 节点速度变化的网络连通度实验
根据上一章提出的基于节点度的整网连通性模型,本章设计仿真实验并配置了 ONE 仿真平台相关参数,实验结束后,根据 Ferry 节点通信记录集得到Ferry 节点邻接矩阵并导入 matlab,计算出区域-Ferry 以及 Ferry-Sink 连通度,最后根据整网连通模型计算出整网连通度。机会传感网络中,Ferry 节点速度越快,Ferry 节点与区域节点、Sink 节点的建立的连接越频繁,感知消息能够在更短的时间内投递至 Sink 节点,网络投递成功率越高,也说明了整个网络的连通程度较高,因此可以通过改变 Ferry 节点速度来模拟三种连通情况(连通度优、连通度良好、连通度差),进行仿真实验。Ferry 节点移动速度变化实验场景如图 5-1 所示。
......................................
5.1.1 Ferry 节点速度变化的网络连通度实验
根据上一章提出的基于节点度的整网连通性模型,本章设计仿真实验并配置了 ONE 仿真平台相关参数,实验结束后,根据 Ferry 节点通信记录集得到Ferry 节点邻接矩阵并导入 matlab,计算出区域-Ferry 以及 Ferry-Sink 连通度,最后根据整网连通模型计算出整网连通度。机会传感网络中,Ferry 节点速度越快,Ferry 节点与区域节点、Sink 节点的建立的连接越频繁,感知消息能够在更短的时间内投递至 Sink 节点,网络投递成功率越高,也说明了整个网络的连通程度较高,因此可以通过改变 Ferry 节点速度来模拟三种连通情况(连通度优、连通度良好、连通度差),进行仿真实验。Ferry 节点移动速度变化实验场景如图 5-1 所示。

......................................
第 6 章 总结与展望
6.1 全文总结
本课题针对机会传感网络链路建立的机会性和随时间演化的特点,采用时空图对 OSNs 连通性进行建模,分别从消息传输角度和拓扑角度定义了相关连通性参数,构建机会传感网络连通性模型。提出了“行程”表征消息的可达路径,接着考虑消息传输时间特性和空间特性,定义出时间距离和拓扑距离并采用Pearson 相关系数对两者的相关性进行了分析,构建整网连通性模型,并采用仿真实验验证了模型的有效性,实验结果表明,该模型能较好的反映网络连通情况,但是模型不能很好区分连通度近似的场景。对该模型进行分析,发现该模型分析角度不够全面,同时鉴于机会传感网络的三层结构,从 Ferry 节点出发,考虑了节点度和节点连接强度,定义出区域-Ferry 连通度和 Ferry-Sink 连通度,将两者结合构建出整网连通性模型。接着,在仿真过程中引入滑动窗口改良了整网连通度计算方法,最终建立不同的实验场景和综合验证实验,验证了模型的有效性,结果表明,该模型得到的网络连通度与消息投递成功率吻合程度较高,也能很好的区分连通度近似的场景。
6.1 全文总结
本课题针对机会传感网络链路建立的机会性和随时间演化的特点,采用时空图对 OSNs 连通性进行建模,分别从消息传输角度和拓扑角度定义了相关连通性参数,构建机会传感网络连通性模型。提出了“行程”表征消息的可达路径,接着考虑消息传输时间特性和空间特性,定义出时间距离和拓扑距离并采用Pearson 相关系数对两者的相关性进行了分析,构建整网连通性模型,并采用仿真实验验证了模型的有效性,实验结果表明,该模型能较好的反映网络连通情况,但是模型不能很好区分连通度近似的场景。对该模型进行分析,发现该模型分析角度不够全面,同时鉴于机会传感网络的三层结构,从 Ferry 节点出发,考虑了节点度和节点连接强度,定义出区域-Ferry 连通度和 Ferry-Sink 连通度,将两者结合构建出整网连通性模型。接着,在仿真过程中引入滑动窗口改良了整网连通度计算方法,最终建立不同的实验场景和综合验证实验,验证了模型的有效性,结果表明,该模型得到的网络连通度与消息投递成功率吻合程度较高,也能很好的区分连通度近似的场景。
本文主要工作:
(1)介绍了机会传感网络基本概念、特点和相关应用,阐述了无线传感网络连通性研究成果和刻画机会传感网络连通性面临的问题;
(2)针对多区域机会传感网络的特点,基于时空图对机会传感网络连通性建模,在感知消息可达性基础上,定义了时间距离、拓扑距离等连通性参数描述节点间连通情况,根据时间距离与拓扑距离构建基于消息传输角度网络连通性模型,并建立仿真场景验证了模型的有效性。
(3)为了解决消息传输连通性模型的缺陷,定义节点度和连接强度,综合机会传感网络的拓扑结构和 Ferry 节点的中心性,将其拓展至机会传感网络中,构建整网连通性模型,采用滑动 窗口办法改良整网连通度的计算方法,建立不同仿真场景验证模型的有效性,结果表明,整网连通度能够在不同场景下准确反映网络连通情况,也能很好的区分连通度近似的网络场景,从而验证了整网连通性模型的准确性和适用性。
(1)介绍了机会传感网络基本概念、特点和相关应用,阐述了无线传感网络连通性研究成果和刻画机会传感网络连通性面临的问题;
(2)针对多区域机会传感网络的特点,基于时空图对机会传感网络连通性建模,在感知消息可达性基础上,定义了时间距离、拓扑距离等连通性参数描述节点间连通情况,根据时间距离与拓扑距离构建基于消息传输角度网络连通性模型,并建立仿真场景验证了模型的有效性。
(3)为了解决消息传输连通性模型的缺陷,定义节点度和连接强度,综合机会传感网络的拓扑结构和 Ferry 节点的中心性,将其拓展至机会传感网络中,构建整网连通性模型,采用滑动 窗口办法改良整网连通度的计算方法,建立不同仿真场景验证模型的有效性,结果表明,整网连通度能够在不同场景下准确反映网络连通情况,也能很好的区分连通度近似的网络场景,从而验证了整网连通性模型的准确性和适用性。
参考文献(略)
