本篇文章目录导航
题目:物联网与区块链结合环境下对数据确认时间的研究
第一章 物联网与区块链结合的研究绪论
第二章 物联网与区块链结合的国内外研究现状
第三章 物联网技术区块链中数据确认时间
第四章 物联网技术区块链确认时间模型的建立
第五章 物联网与区块链结合仿真实验与结果分析
第六章 物联网与区块链结合总结与展望及致谢、参考文献
第五章 仿真实验与结果分析
5.1 仿真实验
本章旨在分析区块链网络中存在攻击节点的情况下,等待不同的确认时间对于抵御攻击节点效果的影响。换个角度讲,即是区块链网络存在一定攻击节点q以及应用对数据不可用的容忍程度r存在一定要求的情况下,理论上该应用至少应等待的确认时间。由于本文所规定的物联网应用是使用实际的以太坊来传输物联网数据的,数据进入到以太坊网络中会作为区块中的交易存在。但本文的实验对象是包含物联网数据的区块,因此不需要带入该物联网数据本身的特性,只要数据所在的区块被挖出后就可以直接计算该数据的确认时间,因而无须对物联网数据的发送频率以及数据大小等参数进行设置。实验分为两部分,第一部分是通过Matlab工具对以太坊区块传播模型进行仿真,首先得到区块在诚实者主链上的概率 随时间的变化关系,与公式(4-1)结合得到至少应满足的确认区块数n1与q,r的关系;第二部分是将利用泊松过程得到区块的平均确认区块数n2随时间变化的关系与第一部分结合,提取使n2大于n1的时间段,最终得到确认时间的最小值。
5.1.1 预估实验结果
由于所研究区块被挖出后的一段时间内空白节点占比较高,网络中极易出现分叉,当区块链出现分叉后,由于分叉区块间会产生竞争,因此某区块被其余分叉区块替代的可能性是很大的。但随着时间的推移,经过一段时间区块会传播至大部分节点,若在该时间内没有出现分叉区块,这段时间内分叉区块出现的概率应呈递减趋势。若区块始终没有产生分叉,则随着分叉概率的下降,区块在诚实者主链上的概率 也应呈现递增趋势。与 的递增对应,由于网络中存在攻击节点,且攻击节点始终在其所创造的攻击链条上挖矿,因此,攻击节点所创造的分叉链条区块数必然会随着时间的推移而增加,保证数据安全至少需要的确认区块数也应为递增趋势。对于最少确认区块,当攻击节点增多时,预计数据不可用的概率随时间的增长呈递增趋势;当数据不可用概率升高时,预期可抵御的攻击节点算力随时间递增。最短的确认时间也应随着攻击算力的增多以及数据不可用概率的增加而递增。
5.1.2 实验环境及参数确定
根据第4.2节传播模型的建立可知模型中需要三个仿真参数分别为网络中总节点数N、区块传播周期T以及对等节点数n,本文从实际的以太坊公链上获取。(一)网络中总节点数N的确定Etherscan[33]是一个针对以太坊的区块浏览器和数据分析平台。本文从Etherscan站点所发布的数据提取并统计2018/12/23至2019/1/22一个月内的每日以太坊在线节点数,并取其平均值8142作为网络中总节点数的取值。
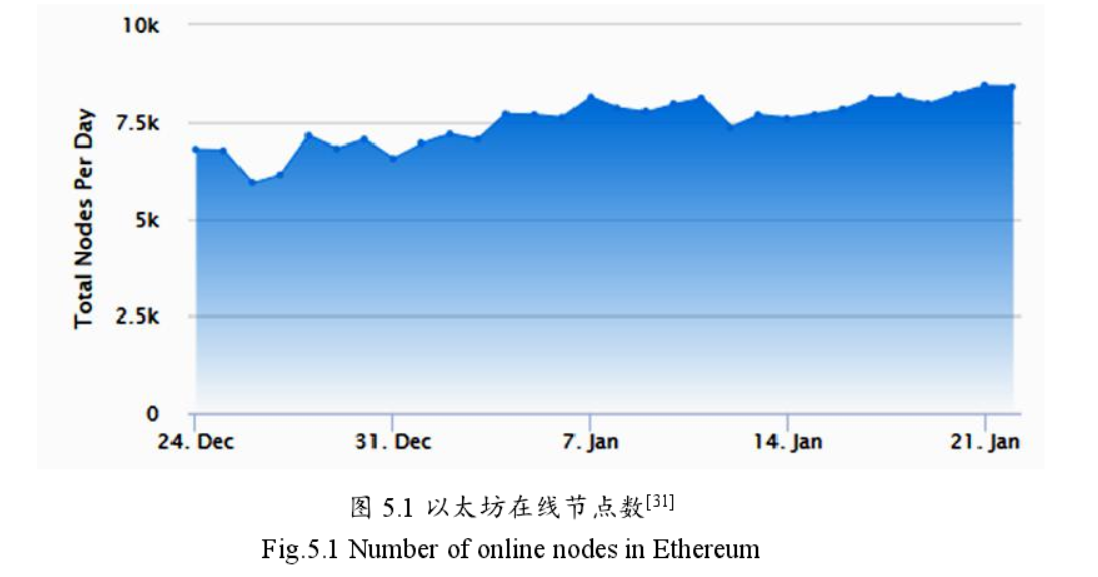
(二)区块传播周期T的确定EthStats[34]是一个用于跟踪以太坊网络状态的可视化平台,它使用WebSockets技术从正在运行中的节点中接收统计信息并通过不同的方法来输出数据,使用者可以通过该网站直观地了解以太坊节点的运行情况。其中包括区块传播时延和节点的对等节点数量。本文提取EthStats中各节点接收区块的平均时延,并使用多种概率分布函数拟合,发现使用对数正态分布拟合的误差平方和最小,区块传播时延T的拟合图像如图5.2所示:
最终得到区块传播时延的概率分布函数如公式(5-1)所示: n nn (5-1)本文以该对数正态分布作为仿真参数在实验中的每个周期依概率提取区块传播时延。(三)对等节点数n的确定提取EthStats.net中各测试节点发现的对等节点数,经过对对等节点数据拟合的实验,对等节点的数量并不满足任意一种概率分布。本文将提取的数据转化为数组,在实验中的每个周期内数组中的元素等概率被选区为节点的对等节点数。
5.2 仿真实验及结果分析
第一部分实验是对最少确认区块数量进行仿真,但通过本文在 3.1 小节的分析,需先得到区块在主链区块上的概率 ,之后带入公式(4-1)进行分析。本文使用 Matlab 仿真工具对以太坊的传播模型进行 500 次仿真实验,统计区块各时刻在主链上的概率,结果如图 5.3 所示:
图5.3表示区块在主链上的概率与时间的关系。图中横轴为所研究的区块在被挖出后经过的时间,纵轴表示区块在诚实者主链上的概率。图线总体呈先骤增再趋于平缓的趋势,并且随着时间地推移概率逐渐趋于1。图线的拐点为第5秒左右。通过图线和数据可以得到:区块在被挖出之后的5秒内,区块在主链的概率递增且具有很高的速率。由得出的数据可知在5秒时概率增加至95.07%,之后概率仍然递增但增长速率逐渐趋于0,概率也逐渐趋于1。由于区块在被挖出后的一段时间内只被少部分节点接收,尚未被网络中大部分区块链节点所认可,因而其在主链上的概率较低。此外该区块在向全网广播的过程中还面临着其他等高度分叉区块对于主链的竞争,当分叉区块出现后,所研究的区块需要等待自身确认区块的出现来超越分叉区块的确认区块数并成为主链区块。本实验给出了在没有攻击节点的情况下,区块等待一段时间后在主链上的概率。换句话说,区块被挖出后经过5秒,区块在诚实者主链上的概率至少为95.07%。通过图像和数据还可以得知:除 之外的其他分叉区块上的数据在 5 秒后在主链上的概率始终低于 4.93%。因此,若应用数据保存在其他分叉区块中,那么随着时间的增加,区块中的数据几乎是不可用的。本文为实验第一部分设计了两组实验来分析应满足的确认区块数在不同的 q 和 r 下的变化趋势以及得出具体数值,详细说明如下:第一组实验测试了应用可以容忍的数据不可用概率 r 分别取值为 10%、5%和 1%下最少确认区块数 n1与时间和攻击节点算力占比 q 的关系。由于当攻击节点占比大于 50%等同于占全网 33%以上,网络已经满足不了拜占庭容错[35],即区块链节点判断不了接收到区块的正确性,导致整个网络无法运作。因此本文将 q 的研究范围规定为 0~45%。由于物联网中在满足高效的数据传输的同时更要保证数据的安全性,因此区块中数据不可用的概率不宜过高,本文将 r 的研究范围规定为 0%~10%。本实验的目的是为对于安全性与时延具有不同要求的物联网应用分别给出其至少应满足的确认区块数。第二组实验测试在不同的攻击节点与诚实节点算力之比 q 分别取值为 15%,30%和 45%时应用至少要满足的确认区块数 n1与时间和数据不可用的概率 r 的关系。q 取 15%、30%、45%相当于攻击节点占全网的 31.03%、23%和 13%。实验的目的是探究在网络环境不安全的情况下,应用等待不同的确认区块数时数据不可用概率的表现情况。第一组实验结果如图 5.4 至图 5.6 所示:
图5.4至图5.6表示给定不同的数据不可用概率下,时间与最少确认区块数的关系,其中横轴表示区块被挖出后经过的时间,纵轴表示最少确认区块数。图线左端的下降趋势是由于在区块在被挖出后的一段时间内,分叉区块产生的概率较高,区块间竞争主链区块的程度也更激烈,此时需要区块在短时间内产生更多的确认区块来保证不被分叉链条超越。而随着时间增长,其他分叉区块的确认区块数也逐渐增加,需要更多的确认区块来维持更大的区块树重量。此外,通过不同攻击节点算力的对比可以看出:不同图线增加区块的间隔时间不同,是由于攻击节点占比越高,在短时间内分叉区块的确认区块增加得越快,因此需要更快速地增加区块。从0时刻起有一段时间的区块数表现为无穷大,其意义是在该时间段里确认数据后数据必然会使得区块中的数据在一段时间后失效。当r=1%时,至少等待56.2秒才能开始确认区块,在此时间内确认区块都是不安全的;当r=5%时,至少需等待20秒;而当容忍度为10%时,等待时长至少为7.75秒。当r固定时,对比不同图线可以发现,增加一个确认区块所需要的时间间隔不同,是由于攻击节点占比越高,在短时间内分叉区块的后续区块增加得越快,所以需要更快速地增加区块。此外,随着q的递增,图线的斜率也依次递增,意味着若攻击者算力增多,诚实者需要更快地增加确认区块数。第二组实验结果如图 5.7 至 5.9 所示:
图5.7至图5.9表示给定不同的数据不可用概率下,确认时间与应满足的确认区块数的关系,其中横轴表示区块被挖出后经过的时间,纵轴表示至少应满足的确认区块数。由于区块数为整数,因此图像呈阶梯状。由图像可知:当q分别为15%、30%和45%时,经过一段时间后才可开始确认区块,而这段时间大致相同,符合实验前的预期。此外,通过对图线斜率的分析,q=15%、30%、45%时分别增加2个、3个、4个确认区块数,就可将数据不可用概率从10%降低至1%。第二部分实验是将实验第一部分与第 4.3 节对实际的确认区块数结合并使用 Matlab 实验得到最短确认时间,实验测试不同的攻击节点算力占比 q 下最短确认时间满足的变化趋势以及不同应用可容忍的数据不可用概率 r 下最短确认时间满足的变化趋势。实验的目的在于得到不同的攻击者算力以及数据不可用概率下能够满足安全条件理论上的确认时间。如图 5.10、图 5.11 所示:
图5.10表示不同的攻击节点算力对应的最短确认时间,其中横轴表示攻击节点与诚实节点算力比值q,纵轴表示最短确认时间。可以发现,随着攻击节点算力的升高,应用需要等待的确认时间也随之升高,且增长率逐渐递增。在区块链网络中攻击节点算力比例小于5%时,数据不可用的概率为r=5%和1%时的最短确认时间几乎都为31.6秒,这是由于以太坊中区块链的自主分叉同样会导致当前的主链区块被其它区块替换。当可容忍的数据不可用概率降低时,确认时间变化率增加。对于5%至45%之间的任意q,通过r=1%和r=10%的对比,可知确认时间提高约2.8倍后,能够容忍的数据不可用概率至少提高至原来的10倍。通过r=1%和r=5%的对比,可知等待时间提高约1.37倍后,能够容忍的数据不可用概率至少提高至原来的5倍。因此,在攻击节点算力增多的情况下,若原先数据不可用概率在10%以内,只要攻击节点算力比例不超过45%,应用将确认时间设置为之前的2.8倍以上足以将数据不可用的概率维持在1%之内。
图5.11表示不同的数据不可用概率对应的最短确认时间,其中横轴表示数据不可用的概率r,纵轴表示最短确认时间。通过观察不同图线得知:攻击节点占比为15%和30%时,最短确认时间在r=40%处同时收敛于15.8秒,可能是由于在攻击节点比例小于30%时攻击节点对数据不可用的概率几乎不产生影响。而在攻击节点占比为45%时,最短确认时间收敛于31.6秒。此外,分析图5.11各图线的最大值可以得知:当攻击节点与诚实节点算力之比分别为15%、30%、45%时,应用分别将确认时间设置为47.4秒、79.05秒以及173.95秒可以使得区块中数据不可用概率维持在5%以内。对于数值在5%至50%之间的任意r,该数据意味着当数据确认时间提高至之前的1.67倍时至少能抵御相当于之前两倍的攻击算力,当数据确认时间提高至之前的3.67倍时至少能抵御相当于之前三倍的攻击算力。
5.3 本章小结
本章对差分形式的阻滞模型进行了实验仿真,最终得到了时间与区块在主链上的概率的对应关系。在此基础上,进一步得到了不同的攻击者算力以及不同的数据不可用概率下应满足的最少确认区块数随时间的变化,并根据所得到的数据进行了分析。最终得到了不同攻击者算力以及不同的数据不可用概率下的最短确认时间。
