本文是一篇机械论文,本文采用物理信息神经网络(Physics-informed Neural Networks,PINNs)与传统启发式AMR的混合框架,将控制方程的残差作为误差指标来指导非结构网格自适应加密。
1 绪论
1.1 研究背景
随着计算机技术的不断进步和流体力学理论的日益完善,计算流体力学(Computational Fluid Dynamics,CFD)成为21世纪流体力学领域的重要技术之一,是一门包含数学、流体力学和计算机科学的混合学科。主要是通过数值模拟技术来求解控制方程,模拟流体在空间和时间上的流动状态,并通过图像或视频展示结果。传统的流体力学至少可以追溯到古希腊时代,当时阿基米德研究流体静力学和浮力。在计算机技术兴起之前,对于流体力学的研究主要依赖于理论分析和实验观测,从宏观的系统层面分析其性质,而非微观粒子层面。然而,随着对相关物理问题的深入研究,传统方法所具有的局限性愈发显著。例如在航空航天这一领域中,对机翼的模拟会涉及到复杂的工况和湍流模型,仅仅使用已知的物理公式是无法在理论方面解决实际工况的,需要通过实验进一步确定,而实验观测一般对于时间和费用的要求较高,难以多次进行重复实验。所以在计算机科学技术得到迅速发展之后,由于计算流体力学本身的灵活性、经济性和适用于各种复杂流动工况等优势,得到了更多科研工作者的认可并且逐步在流体力学领域中发展成为了一门优秀学科,并被广泛应用在各类复杂的实际问题中。面对无法使用理论知识解决的问题,CFD可以充分发挥其优势,将问题转换成数值解的格式进行模拟。若是对比实验观测方法,CFD技术仅仅需要在计算机上进行模拟,极大程度上节省了人工时间,显著降低实验成本,并且可以在过程中根据需要更改条件,避免一些重复性的工作。
........................
1.2 自适应网格加密
关于自适应网格加密技术的相关工作,最早可以追溯到上世纪八十年代。1984年,Berger与Olige最早提出了自适应网格法[7],该方法抛弃了均匀网格,采用了能够自动适应所求解问题中解的特征的不均匀的网格。自适应网格加密技术发展至今,根据加密方式的不同被分为三类:重新分布网格节点位置(R型)、计算函数升阶(P型)和本文使用的局部加密(H型)[8]。
在计算机性能受到限制的早期阶段,计算时网格的数量不能过多,因此对网格点的分布要求较高,当时大多数采用R型自适应网格加密技术。R型自适应方法的核心思想在于维持网格节点的数量以及拓扑间的连接关系恒定,借助特定的控制策略对节点的空间坐标予以调整,让节点能集中分布在流场中某个物理量的高梯度区域,在剩余区域的节点分布则相对稀疏,减少网格数量[9]。R型自适应网格加密的主要步骤是首先依据计算初始网格获取的流场结果来对网格节点的坐标进行调整,从而得到新的网格。此方法的优势在于仅仅需要变更网格节点的空间坐标分布,在提升数值解精度的同时,计算量基本保持不变。不过由于存在拓扑连接不可变的这一限制,网格节点的移动受到较大的约束。若是相对复杂的网格区域,设计有效的节点移动策略难度显著增加,既需要兼顾移动效果又要防止网格错误[10,11]。在微分方程数值解领域,移动网格方法得到广泛应用,但在CFD(计算流体动力学)领域的应用会受到限制。主要因为流场方程计算相对复杂,通常需要专门的流场求解器进行处理,难以将移动网格节点与流场方程求解耦合。此外,CFD的计算网格相对复杂,需要考虑物体的复杂外形和大范围的求解域,而不同于大多数偏微分方程求解可以简单地使用均匀网格。
......................
2 Delaunay网格加密及机器学习模型
2.1计算网格
2.1.1 计算网格介绍
计算流体力学中几乎所有的离散数值方法都与网格有关,其最终求解也是在网格上实现。将应用于CFD计算的网格称为计算网格,随着应对问题的复杂程度发生变化,物理问题越复杂,对使用的计算网格要求也会更高。为了方便后文叙述清晰,在实行自适应网格流程前的网格定义为初始网格,自适应网格加密不仅仅一次,按照等级划分,每一次加密就是一个等级,初始网格定义为等级1,所有自适应加密结束得到的网格为最终网格,当进行新一轮加密后得到的流体数值解与加密前等级的数值解基本不变时,称加密前的那个等级的网格为最优网格。
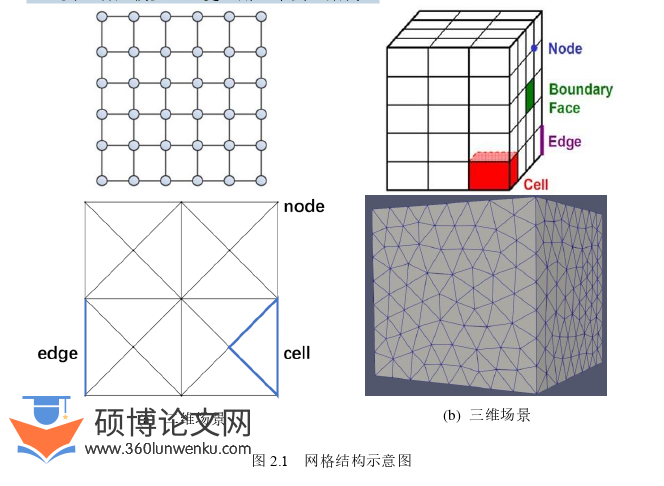
网格从元素组成上主要分为:单元(cell/mesh)、面(face)、边(edge)、节点(node)和区域(zone)。图2.1以结构网格和非结构网格分别为例展示了它们在二维场景和三维场景下的示意图。点连接成线,线集合成面,面汇聚成体。网格单元指的如图2.1(a)中的三角形和四边形,以及图2.1(b)中的四面体和六面体。在二维场景下,面是由线段组成的,区域则是由一组节点、边和单元组成的。结构网格一般均是由规则的四边形网格相邻组成的,其优点在于网格质量高,有利于降低网格单元数;而缺点是难于处理表面复杂的几何,划分时间较长。而非结构网格的内部节点的相邻单元均不相同,网格间无规律地分配在各个位置,优点是灵活性较大,能处理任意复杂表面,缺点是对于网格的质量要求较高,容易因为分布导致网格发生挤压问题。本文所应用的主要是非结构三角形网格,对于此类的研究较少,且更适用于本文的案例。
机械论文怎么写
.........................
2.2 Delaunay网格加密
2.2.1 Delaunay三角剖分
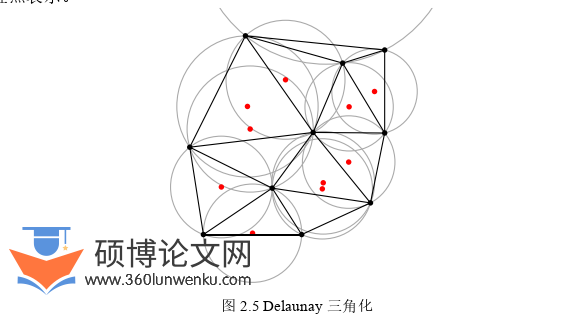
Delaunay三角剖分算法最早是由1934年前苏联数学家Delaunay提出的[62],旨在生成多边形网格,其核心在于:在任意给定的平面内,无论点集如何排布,都保持着空圆特性以及最大化最小角特性,使空间内只存在一种三角剖分算法。空圆特性是指Delaunay算法会保证内部生成的网格单元是唯一的,只能是三角形网格,且三角形网格中心的外接圆范围内不会出现其它三角形网格上的节点。另外Delaunay三角剖分产生的网格的最小内角大于任意非Delaunay三角剖分产生的网格的最小内角,从而确保不会有某个三角形的内角过小使得三角形偏移量较大的情况[63-65]。总结以上内容,Delaunay三角剖分算法最适用于三角网格的生成。一个平面Delaunay三角化的例子如图2.5所示,所有三角形外接圆的圆心以红点表示。
机械论文怎么写
设平面内的散点集为????={????0,????1,????2,⋯,????????},共有n个点,其中????0为整个集合P中索引最大的点,在二维平面空间????2内选取位于集合P以外的两个点,定为点????−1和点????−2,连接点????−1、????−2和????0,组成一个大的三角形区域,包含着集合P中除了????0以外的所有点。然后可以逐一插入点集P中的其余点,随着点的加入而形成新的三角形,其中插入的点所在位置会有两种情况:落在某个已经形成的三角形的内部或者某条边上[66]。第一种情况如图2.6(a)所示,当点????????在某个三角形内部时,会将其与所在三角形的三个顶点连接起来,形成新的三个三角形;第二种情况如图2.6(b)所示,当点????????在某个三角形的边上时,会识别与这条边有关联的三角形,并将其与对应的两个三角形的顶点连接起来,形成新的三角形。但是需要注意到是,会有的散点形成的三角形偏移过大或者过小使得不遵循Delaunay三角化的准则,从而影响计算结果,因此需要检查生成的网格情况,判断其网格质量是否合格[67,68]。
..................................
3 控制方程及数值计算方法 ................. 31
3.1 控制方程及其无量纲化 .................. 31
3.1.1 二维不可压缩Navier-Stokes方程 ...................... 31
3.1.2 方程的无量纲化 .................... 32
4 基于物理信息神经网络的翼型自适应网格加密 .................. 51
4.1 数值模型和边界条件 .................................. 51
4.2 传统自适应网格加密—翼型 ................................. 55
4.3 基于物理信息神经网络的自适应网格加密—翼型 .................... 59
5 总结与展望 .................................. 71
5.1 本文总结 ........................................... 71
5.2 未来展望 ....................................... 72
4 基于物理信息神经网络的翼型自适应网格加密
4.1 数值模型和边界条件
翼型是指机翼、螺旋桨叶片、风机叶片等飞行器或流体机械部件的横截面形状。翼型的设计和性能对于飞行器的升力、阻力、飞行效率和稳定性等方面具有至关重要的影响。早期的翼型研究可以追溯到 19 世纪末期,当时人们主要通过实验方法来探索不同形状翼型的气动特性。随着航空工程的发展,理论分析和计算方法逐渐得到应用。经典的翼型如 NACA(美国国家航空咨询委员会)系列翼型,在航空领域被广泛研究和应用。20 世纪中叶以来,随着计算机技术和计算流体力学(CFD)的迅速发展,翼型的设计和优化过程变得更加高效和精确。研究人员能够更深入地理解翼型周围的流场特性,从而设计出具有更好性能的翼型。
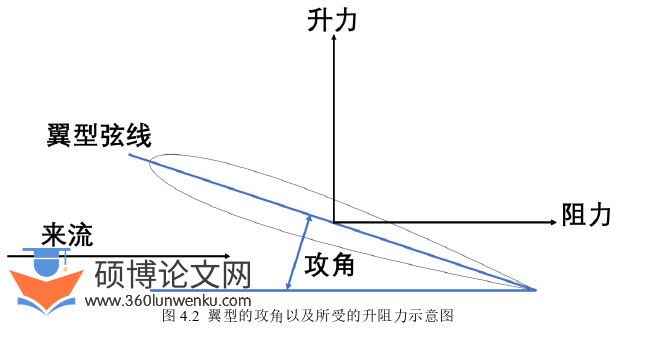
本章中数值计算模型选用的是经典的NACA 0012翼型,其特征是厚度与弦长比为12%的对称轮廓,其基本轮廓的数据来自NACA(美国国家航空咨询委员会)官方网站,给与的是轮廓上各个节点的坐标,于是需要将其连接起来组成翼型的基本形状,如图4.1所示。翼型研究中的主要参数是升阻力和升阻力系数。阻力定义为流体流经物体时,产生的阻碍物体运动的力,一般与物体的运动方向相背。升力定义为流体流经物体表面时产生的、垂直于流向的力。阻力系数(????????)是一个无量纲系数,用于量化物体在流体环境中受到的阻力。升力系数(????????)则是与翼型的升力、翼型周围流体的动压以及翼型的参考面积相关的无量纲系数。攻角定义为翼弦与来流之间的夹角,如图4.2所示,是研究升力系数和阻力系数变化的重要几何参数。
机械论文参考
.........................
5 总结与展望
5.1 本文总结
在科学计算和工程领域中,准确有效地模拟物理现象一直是一个重要的挑战。传统的数值方法在处理复杂的物理问题时,常常受到网格分辨率的限制,导致计算精度不足或者计算成本过高。为了解决CFD的模拟精度问题,提出了自适应网格技术,包含P型自适应、H型自适应以及R型自适应网格。但是由于流场结果的复杂性,在应用自适应网格加密技术也会有产生大量网格的问题。本文研究了一种基于物理信息神经网络(PINNs)的自适应网格加密技术,导入CFD计算网格以及计算结果,使用PINNs用于流场预测,可以应对不同雷诺数下的层流问题,通过残差的大小来标记网格节点,相比于传统的自适应网格技术,有效控制了加密的网格数量,并能保持较高的计算精度。本文的主要工作如下:
(1)研究了常见的网格加密方法,网格的加密方式多种多样,根据网格类型的不同,选择的加密方式也有区分。Delaunay三角剖分适合用于在二维平面,将随机散点生成三角网格,符合本文的工作,使用网格最大面积约束加密方法来确保网格的质量,无论是规则物体还是不规则物体,该方法都能在一定程度上保证加密后的网格质量,将其应用在真实流场的算例上,结果显示可以得到精确的数值结果。
(2)基于物理信息的神经网络(PINNs)是在传统的人工神经网络的基础上进一步衍变而来的,其主要形式是将物理规律以偏微分方程的形式融入到神经网络的训练过程中,通过这种方式,使得网络能够有效学习并获取符合物理规律的解,能显著提高神经网络的准确性,并能应对多种复杂的流场情况。在自适应网格加密方面,PINNs展现出了显著的优势,能优先捕捉梯度较大的区域,从而避免了使用过量的网格。
参考文献(略)
