本文是一篇工程管理论文,本文以末端携带工具的六轴协作机械臂作为研究对象,针对其在3C行业电路检测任务中占据重要地位的末端定位技术进行研究:建立了运动学与动力学模型;对末端携带工具的机械臂系统进行了手眼标定与工具坐标系标定;对轨迹规划进行分析,研究多项式插值实现生成最优定位轨迹;采用神经网络与非奇异快速终端滑模面设计了机械臂运动控制器,实现在不确定性影响下的高精度轨迹跟踪;并针对上述研究设计实验验证研究结果。
第一章绪论
1.1课题背景与研究意义
随着制造业和信息技术的飞速发展,中国工业自动化的水平达到了一个新的高度。在“中国制造2025”国家战略推动下,机器人在当今工业生产中已经成为不可或缺的一部分,广泛应用于各个领域如汽车制造、电子产品组装、码垛搬运等[1]。传统的工业机器人通常被用于重复性高、危险性大或者精度要求高的任务,能够在生产线上高效地完成单一任务,提升生产效率和产品质量[2]。但工业机器人也存在一定局限性,主要体现在其安全性、灵活性和易部署性等方面[3]。传统工业机器人通常需要在封闭的安全围栏内运行,以防止与人员发生意外接触,这极大地限制了其在3C、医疗、家庭服务等行业的发展。

工程管理论文怎么写
.........................
1.2国内外研究现状
1.2.1机械臂定位技术研究现状
机械臂标定主要是通过物理约束[8]-[10]、机器视觉标定[11]-[17]的方法。物理约束以确定空间的平面或点集为约束,通过计算实际偏差求解运动学参数模型,完成辨识。基于机器视觉的机械臂标定,通过机械臂、相机和靶标构成辨识系统,相机不断获取靶标的相对位置,与其理论位置对比完成参数修正。中国计量大学的喻靖[18]针对传统的协作机械臂末端执行器即时定位效果差的问题,采用AprilTag标签定位,提出一种基于几何学提取ROI的快速定位算法。张彦泽[19]等为满足机械臂末端精确定位的需求,提出了一种适用于“眼在手上”机械臂-相机系统的自适应扩展卡尔曼滤波方法,实现对运动噪声协方差矩阵的精确估计进而实现对机械臂末端运动的精确估计,但仅仅对该算法进行了仿真验证,缺乏进一步的实验数据支撑。刘文婧[20]提出一种机械臂辅助机器视觉系统,该系统能够实现对工件的图像采集并进行预处理,通过改进的Canny轮廓的提取算法与基于Hausdorff距离的模版匹配完成对不同种类工件进行识别和定位。该方法是针对工件定位设计,定位精度可达0.35mm,但无法满足精度要求更高的定位任务。
综上所述,协作机械臂末端定位是一项十分复杂的技术,为了满足最终的定位任务需求,仅仅提升绝对定位精度远远不够。机器视觉标定方法中引入了相机,并且机器进行自动化作业时,协作机械臂末端往往携带工具。因而还需要提升手眼标定精度与工具坐标系标定精度。在所有标定任务完成后,为了使机械臂定位轨迹更平滑,定位过程到达时间更短以及提升定位中抗干扰能力,还需要对机械臂定位轨迹进行规划与跟踪,进而完成协作机械臂末端定位任务。
............................
第二章协作机械臂末端定位技术基础
2.1 Udwadia-Kalaba理论与李群李代数基础
2.1.1 Udwadia-Kalaba理论
视觉引导的协作机械臂末端定位技术是一种通过手眼标定、工具坐标系标定、轨迹规划以及轨迹跟踪等复杂功能,实现协作机械臂末端工具在操作过程中精准定位的技术。本章首先介绍了在协作机械臂手眼与工具协同标定与轨迹跟踪研究中涉及的Udwadia-Kalaba理论与李群李代数理论,为后续运动学与动力学的研究奠定基础。机器人运动学是研究机器人在空间中运动规律和姿态变化的学科,为协作机械臂的手眼与工具协同标定、轨迹规划等方面提供了重要的理论依据。机械臂动力学是研究机械臂在运动过程中的力学特性和动态行为的学科,为协作机械臂的轨迹跟踪和控制提供了重要的理论支撑。
李群是一个拓扑群,是一个光滑可微流形。一个刚体能够在空间连续的旋转运动,故可以用李群表示刚体在空间中的位姿信息[67]。常用的李群主要有:特殊正交群,用于描述旋转;以及特殊欧式群,用于描述位姿变换。而每一个李群都有一个与之相对应的李代数,李代数描述了李群的局部性质。
...........................
2.2机械臂运动学与动力学建模
2.2.1机械臂运动学建模
D-H参数法(Denavit-Hartenberg parameters)是一种在机器人学中广泛应用的方法,用于描述机器人关节之间的几何关系。通过定义连杆长度、连杆偏移、连杆旋转角度和连杆旋转角度的初始位置等四个参数,D-H参数法构建了一个连续的坐标系链,能够准确描述机器人关节的运动。该方法简单易懂,可用于正逆运动学计算、机械臂标定、轨迹规划等任务,同时也为机器人姿态估计和运动仿真提供了便利。
D-H参数的含义:
(1)连杆长度????????:定义为从????????−1移动到????????的距离,沿????????轴指向为正。其实质为公垂线的长度。
(2)连杆转角????????:定义为从????????−1旋转到????????的角度,绕????????轴正向旋转为正。
(3)关节偏距????????:定义为从????????−1移动到????????的距离,沿????????−1轴指向为正。其实质为两条公垂线之间的距离。
................................
第三章基于矩阵降维的线性协同标定算法...............................23
3.1手眼标定和工具坐标系标定.............................23
3.1.1工具坐标系标定方法........................23
3.1.2手眼标定方法.....................................26
第四章基于李代数扰动模型的非线性协同标定算法..........................39
4.1李代数求导与左乘扰动模型.............................39
4.1.1 BCH公式及其近似形式...............................39
4.1.2李代数求导..................................40
第五章基于U-K理论的轨迹跟踪控制..........................50
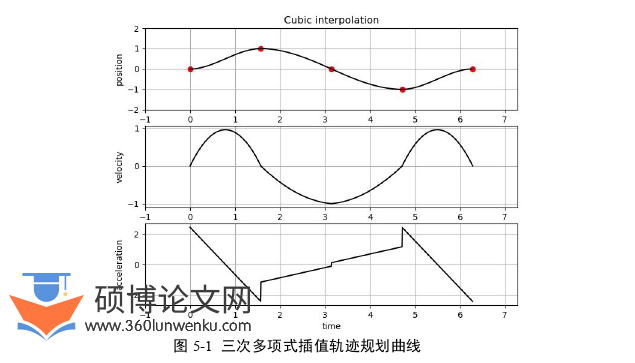
5.1多项式插值轨迹规划................................50
5.1.1三次多项式插值法...........................50
5.1.2五次多项式插值法...................................51
第五章基于U-K理论的轨迹跟踪控制
5.1多项式插值轨迹规划
在协作机械臂末端定位任务中,轨迹跟踪所需的理想目标定位轨迹来自于轨迹规划。在获得精准的标定结果后,为了使协作机械臂可以精准迅速的从工作零位定位到目标位置,本节采用成熟的多项式插值法对协作机械臂进行定位轨迹规划。
多自由度机械臂是高度非线性的复杂系统,并且往往处于相对复杂的工作环境。因此不管是内部存在的测量与建模误差还是外部存在的环境干扰都会导致机械臂控制精度下降。为了使机械臂在扰动中依然可以顺利完成定位任务,在标定结果可以使末端定位满足精度要求后,需进一步优化定位过程中机械臂的轨迹规划控制,使机械臂拥有平滑的运动轨迹,降低机械臂的损耗。在获取平滑的目标轨迹后,为了确保定位过程按照理想轨迹运行,首先基于U-K理论对机械臂动力学建模,并结合自适应神经网络设计了滑模控制器进行轨迹跟踪控制。为了削弱抖震,改进超螺旋算法并设计新型趋近率函数。然后,构建Lyapunov函数证明闭环系统的稳定性。最后,进行仿真实验,验证算法有效性。
工程管理论文参考
............................
第六章总结与展望
6.1本文工作总结
本文以末端携带工具的六轴协作机械臂作为研究对象,针对其在3C行业电路检测任务中占据重要地位的末端定位技术进行研究:建立了运动学与动力学模型;对末端携带工具的机械臂系统进行了手眼标定与工具坐标系标定;对轨迹规划进行分析,研究多项式插值实现生成最优定位轨迹;采用神经网络与非奇异快速终端滑模面设计了机械臂运动控制器,实现在不确定性影响下的高精度轨迹跟踪;并针对上述研究设计实验验证研究结果。论文主要工作如下:
(1)协作机械臂以相机当作“眼睛”进行自动化作业时,末端工具标定与“手眼”标定分开进行会造成误差累积。针对该问题,本文将空间同一点通过不同回路转移到基坐表系下,利用该点不同的数学表达式构建标定模型。然后将未知量的真实值拆解成初始值加补偿项的形式。针对补偿项,利用微小量假设与李代数理论设计了利用最小二乘求解的线性共同标定法,并设计定位实验,将其与传统手眼标定和工具坐标系标定精度进行对比,结果表明线性协同标定算法最终定位误差均值为0.7914mm,相较于分离标定定位精度提升了43.8%。
(2)针对手眼矩阵的精度对于标定结果具有显著影响,线性协同标定算法面对3C电路板更小尺寸测点精度不足的问题,本文设计非线性协同标定算法并设计实验流程进一步提升定位精度。首先通过平面法操作步骤获取工具坐标标定初始值与二维手眼矩阵初始值,并结合算法获得拍照高度、补齐三维手眼矩阵初始值。然后,利用泰勒公式设计标定误差价值函数,并李代数左乘扰动模型对手眼旋转单独迭代求解。最后根据设计的实验流程完成实验验证。结果表明,非线性法最终定位误差均值为0.3777mm,相较于线性法定位精度提升了52.27%。
参考文献(略)
