本文是一篇软件工程论文,本文首先介绍了神经网络的参数搜索以及架构搜索的研究背景,目的意义以及研究发展现状,接下来分别介绍了提出改进的优化神经网络参数搜索的方法,优化神经网络架构搜索的方法以及最终加速评估神经网络架构的方法,经过实验表明提出算法的有效性。
第一章绪论
1.1研究背景与意义
在最近十几年中,随着大数据技术的发展、各种音视频设备的广泛应用、海量数据的获取,人工智能技术得到了较好的发展和应用背景,在国民经济和社会发展中的作用越来越突出的地位。世界各国政府纷纷出台重要政策和文件争夺人工智能发展的战略高地。例如,在国外,美国于2016年出台了《国家人工智能研究与发展战略规划》;在国内,国务院于2017年出台了《新一代人工智能发展规划》。国内外学术界也掀起了对人工智能的研究热潮,许多人工智能分支方向得到了进一步的发展。其中,演化计算和机器学习作为人工智能领域的两个重要发展分支,旨在加速机器学习在各行各业中应用的自动化机器学习。在这一发展方向中,深层神经网络的自动化学习占据着研究的主体地位。目前,由于演化计算技术在求解组合优化问题和数值优化问题上具有较好的全局优化能力,因此,在神经网络自动化学习中发挥着比较突出的作用,受到越来越多研究者的青睐。演化神经网络的研究正朝着越来越广泛、深入的方向发展,成为了人工智能领域的一个前沿热点研究方向。
随着Alphago机器人的出现,并战胜世界围棋冠军后,神经网络再度成为研究热点。神经网络可以应用于分类、语音识别、自然语言处理等很多领域。本文主要研究如何优化神经网络的性能,由于神经网络性能主要由参数与架构决定的[1],所以本文结合演化计算从这两个方面展开研究。首先,近年来,许多CNN的变体被提出,如Alexnet[2],VGG[3],ResNet[4]等,并且他们使用的都是反向传播技术更新参数,但是由于描述神经网络训练问题的目标函数是多模态的,因此,梯度下降策略易陷入局部极小值[5]。为了避免这一问题,可以使用全局优化技术,如遗传算法(GA)[6],粒子群算法(PSO)[7]和蚁群优化算法(ACO)[8]等。其优点如下:在不考虑初始值设定的情况下,寻找一个多模态函数的全局最小值,并且它们在算法开始时需要设置的参数数量少,算法收敛速度快。这些演化计算方法都有良好的全局搜索能力但都有着对局部最优的不敏感性[9]。将两种方法结合使神经网络性能更佳并有着良好的应用前景[10]。
.................................
1.2国内外研究现状、水平以及发展趋势
1.2.1神经网络参数搜索
在神经网络参数搜索领域中主要有两种方式。第一种是基于梯度的搜索方式,BP算法是其中使用最广泛的一种,其中,学习率和动量因子是梯度下降技术的关键,BP对这些参数很敏感。如果学习率太小,学习就会变得缓慢,如果学习率太大,算法可能无法收敛到所需的满意度。此外,高动量因子导致超调极小值的高风险,低动量因子可能避免局部极小值,但收敛缓慢。经典的BP算法速度慢,且有陷入局部极小的趋势[15]。与BP不同,另一种二阶方法,称为共轭梯度(CG)[16],可用于权重优化。CG不会以梯度向下进行;相反,它会利用一阶导数信息向与前一步方向共轭的方向移动,换句话说,当前步骤对应的梯度保持垂直于前面所有步骤的方向,并且每个步骤至少与前一步相同。这一系列步骤是不相互干扰的。因此,在一个步骤中执行的最小化不会被任何进一步的步骤所取消。它们有几个局限性。例如,它们有陷入局部极小值的趋势,并且它们只用于优化FNN权重。并且,梯度下降算法主要依赖于误差函数,如均方误差或平方误差之和。例如,像高斯-牛顿和最小二乘法只有当代价函数是平方误差之和时才起作用。牛顿方法必须计算Hessian矩阵,它必须是正定的,计算Hessian矩阵需要的资源昂贵。同样,拟牛顿和CG方法需要使用一种行搜索方法,这种方法的计算有时可能很昂贵。
第二种神经网络参数搜索方式是无梯度的搜索方式,其中主要有遗传算法(GA),粒子群算法(PSO)和蚁群优化算法(ACO)等演化计算方法(EC)。由于不需要计算误差函数的梯度信息,它具有良好的全局搜索能力和学习近似最优解的特点。EC以其特殊的自然演化规律和种群优化搜索的优越性为解决问题提供了新的思路和方法。它们主要有以下优点:(1)、EC能快速可靠地解决难题。因此,它们适用于大型、复杂、非连续、不可微和多模态的评价函数。(2)、EC方法是一种通用的方法,可以直接与现有的模拟和模型接口。EC是可扩展的,易于交叉衍生后代。(3)、EC是定向随机全局搜索。它们可以达到几乎最优或全球最大值。(4)、通过同时评估多点,EC具有固有的并行性。与无梯度算法相比,梯度算法局部范围内的搜索能力更加优秀,可以结合两种技术获得更强大的代表和解决实际问题的能力[17]。
...........................
第二章相关研究工作
2.1.神经网络参数搜索
2.1.1参数初始化
通常,主要采用三种初始化方法来初始化神经网络[12]的权值。第一种方法使用固定常数来初始化连接权值,如零初始化器。由于权重是用相同的值初始化,它会导致梯度信息的消失。第二种方法是分布初始化器,如高斯分布和均匀分布。这种初始化器是基于一种随机方法,它有效地避免了第一个初始化器的不足。但该方法存在不同分布条件下的参数选择问题。为了解决这个问题,提出了第三种基于先验知识的方法,如Xavier初始化器[46]。Xavier初始化器使用了一个基于神经元饱和先验的均匀分布范围。由于第二种方法易于实现,应用广泛,本文采用该方法对全连通神经网络参数的初始化。
2.1.2自适应机制
在过去的几十年里,自适应机制在演化计算领域的应用引起了许多学者的注意,并提出了一些有效的[47][48]算法。例如,Qin等人[49]在差异演化(DE)中引入了一种自适应机制,并提出了一种自适应DE(SaDE)。实验结果表明,SaDE能获得质量较好的溶液。此外,Sk.Islam等[50]提出了一种新的DE变体,其中包括一种新的突变策略和参数自适应方案。他们在25个标准基准上将他们的算法与两种经典和四种最先进的DE算法进行了比较。结果表明,该方案大大提高了DE的性能。他们还证明,如果他们的策略与现有的DE变体自适应地集成,性能将得到提高。近年来,Xue等人[48][51]提出了许多基于自适应机制的改进优化算法来解决现实世界中的不同问题。文献[52]中,Sh.Gupta等人提出了一种基于正弦余弦量的修正正弦余弦算法(m-SCA)。它们使用相反的数字来生成相反的总体,这样m-SCA就可以避免局部最优。此外,他们还添加了自适应组件来利用所有有前途的搜索空间。该算法在23个著名的基准任务和5个工程优化任务上进行了测试。计算结果表明,该算法能更有效地求解实际问题。
................................
2.2神经网络架构搜索
2.2.1基于全局的设计方式
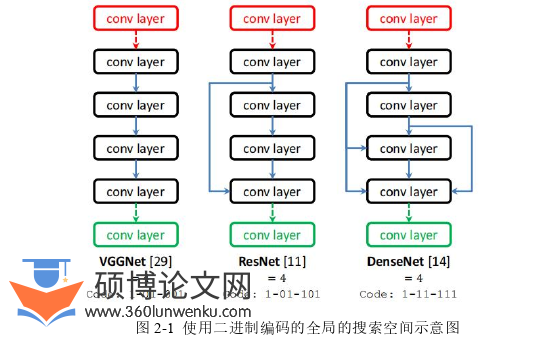
基于全局的搜索空间是通过使用特定的表示方式直接使用基本操作表示出整个网络的结构,如图2-1所示。Real等人在这方面做了初步的工作[28],他们固定模块之间连接方式为线性连接和部分跳跃连接,然后采用大规模变异操作搜索基本模块,例如随机添加、修改或删除包括卷积核、ReLU激活函数、批量归一化层、跳跃连接等在内的组成元素。这项研究的搜索空间自由度很高,几乎能够覆盖大部分现有的骨干网络,能够表示所有具有跳跃连接的线性网络,但是也正是因为自由度过高导致搜索的时间需要上千块GPU同时运行数天。例如,Xie等人[31]采用固定的5×5的卷积核和最大值池化层,采用遗传算法搜索模块之间的拓扑结构,其搜索空间仅为限定大小卷积核下的不同连接结构的网络集合。相反地,Sun,Xue,Zhang等人[12]尝试使用VGGNet的构建方式进行搜索空间设计。他们直接表示出网络的总体结构并进行网络结构的搜索,在搜索过程中总体上采用线性结构,加入少部分的跳跃连接从而达到防止梯度消失的目的。由于直接使用了基本操作,这些方法搜索到的结构多样性十分丰富,但是同时带来的问题是时间开销非常大。
软件工程论文怎么写
..............................
第三章基于全连接神经网络的自适应梯度下降搜索算法..........................17
3.1概述...................................17
3.2神经网络优化模型..................................17
第四章基于块的自适应变异神经网络架构搜索............................33
4.1概述.....................................33
4.2算法描述.......................................33
第五章基于分割演化块的神经架构搜索研究.............................47
5.1概述............................................47
5.2算法描述.......................................47
第五章基于分割演化块的神经架构搜索研究
5.1概述
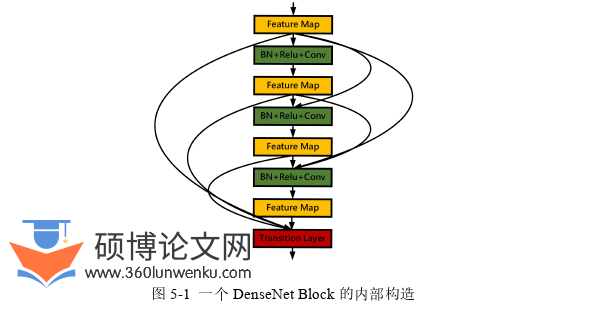
在架构搜索过程中,评估一个个体所消耗的计算资源十分昂贵,这是由最终搜索到的模型架构的复杂度以及数据集规模决定的,即使在限制了搜索空间的情况下,通常一个完整的NAS过程需要多块GPU进行十几天的搜索才能完成,昂贵的计算资源和消耗的时间成本也是十分巨大。当前使用比较广泛的早停机制,削减数据集与削减种群的方式都会造成一定的个体评估偏差,所以本文压缩搜索空间,减少每个个体的编码长度,以提高算法的搜索效率。并提出一种切割方法,在保证最终分类精度的同时,大大减小了最终搜索模型的大小和计算资源消耗。利用切割方法得到的最终模型不需要重新演化,它可以转移到其他数据集。从而最终缩减评估时间。
软件工程论文参考
...........................
第六章总结与展望
6.1工作总结
本文首先介绍了神经网络的参数搜索以及架构搜索的研究背景,目的意义以及研究发展现状,接下来分别介绍了提出改进的优化神经网络参数搜索的方法,优化神经网络架构搜索的方法以及最终加速评估神经网络架构的方法,经过实验表明提出算法的有效性。本文主要工作如下:
(1)为解决反向传播算法易陷入局部最优的问题,并且其效果极大的受到梯度下降策略中超参数选择的影响,本文提出一种基于种群的自适应梯度下降搜索算法来搜索神经网络的参数。算法自动设计不同阶段的学习率来匹配不同的搜索阶段并将其分别加入策略池,无需人为调参优化效果,并且在11个UCI数据集上证明了提出的算法的全局寻优能力。
(2)为解决已有架构搜索过程中搜索策略单一以及演化信息丢失的问题,本文提出一种基于块的自适应的变异策略的遗传算法来进行神经网络架构搜索,提出了三种架构变异算子,并使用自适应机制根据初期经验指导后续演化,在CIFAR10和CIFAR100上证明了提出算法的有效性,并且丰富搜索过程中的种群多样性的同时,加大搜索到最终新型架构的概率。通过前期经验的指导,使后期演化的最终架构更具竞争性。
(3)为解决搜索过程中每次个体评估时间过长的问题,本文压缩了搜索空间,并提出一种渐进式切割块的方式,在保证精度的前提下,减少参数量,压缩模型大小,有效加快评估速度和减少计算资源的消耗。
参考文献(略)
