本文是一篇土木工程论文,本文通过理论推导、案例分析以及有限元计算结果对比分析,对研究对象的连续化分析方法和有限元建模方法等方面进行了研究,提出两种钢筋混凝土空腹夹层板新型建模计算方法。
第一章 绪论
1.1 引言
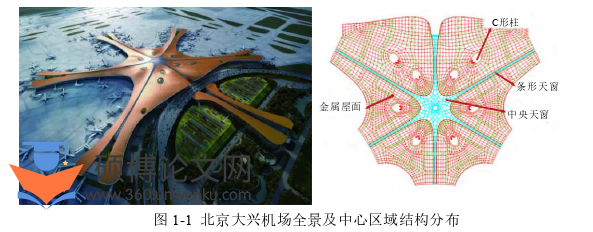
随着中国式现代化进程的推进,人民生活质量日益提高的同时也逐渐有了新的物质精神追求。人们学习工作之余去体育场馆强健体魄,或是去音乐厅放松身心,还是在高铁大厅里等待旅游出行等,美好的生活离不开这类能提供较大空间的设施,而这样的建筑需求也促进了空间结构的发展[1-4]。由我国设计建造的北京大兴国际机场于2019年下旬正式通航,其航站楼中心区屋盖平面尺寸达到545m×445m,屋盖投影面积约18万平方米[5, 6]。为满足航站楼空间大、少柱的建筑功能要求,设计团队采用支承体系与屋盖结构一体化的巨型网格结构,如图1-1所示,仅有8个C形柱处于靠近中心区域,完美协调了整体建筑的设计美观和空间利用。该航站楼结构新颖,设计施工难度巨大,获得了代表中国建筑行业工程质量最高荣誉的中国建设工程鲁班奖,被誉为“世界新七大奇迹”之一[7],是我国运用大跨空间结构建设航空口岸的重要里程碑。
土木工程论文怎么写
.......................
1.2 空腹夹层板结构的发展
1.2.1 钢筋混凝土空腹网架结构
贵州工学院的马克俭教授于1984年提出了钢筋混凝土空腹网架结构体系[1],该体系的主要建筑材料为钢筋混凝土,造价更低的同时也免去钢网架结构的维护费用,取材与施工更加方便,适合于屋盖和楼盖结构。由于我国早期的空间网格结构选择有限,无论工业建筑或民用建筑都首选使用钢网架结构进行建造。但当时我国的钢铁产能不足,导致钢网架结构的工程造价高昂,根据计算其在跨度低于30m时的经济指标劣势尤为明显;工业与民用建筑尚对30m以上跨度的需求较小,更多需求的跨度在18m至30m这一区间,选择钢网架结构进行建设很不经济,特别是在我国经济条件的更加贫瘠中西部地区,钢网架结构的使用愈发困难。
考虑到以上以及贵州环境等多方面问题,马克俭教授提出了这一结构体系。空腹网架由上下弦杆与竖向的竖杆组成,与网架结构不同的是空腹网架极少使用斜腹杆。其突出特点是竖杆长细较大且整体板厚较大,腹杆主要以承受轴力及弯矩。
贵州省总工会工人疗养院食堂(1985年)采用此结构体系进行建造楼盖和屋盖,跨度达到11m,是我国首次建成的钢筋混凝土空腹网架结构建筑。经过中国土木工程学会空间结构委员会在1985年的技术鉴定,结果为“结构安全、合理、经济,适用于30m以下的公共建筑”。据统计,在随后18年内建成应用的空腹网架屋盖和楼盖结构项目有20余项,总建筑面积达到50万平方米。于1987年采用该楼盖结构年建成的安顺市体育局训练馆,平面尺寸达到42m×24m,在2020年(图1-2)回访时仍正常工作[15],可见此结构的安全性。
...........................
第二章 基于高精度等效剪切模量的连续化分析方法研究
2.1 两种连续化分析方法简介
钢筋混凝土空腹夹层板因其独特的构造形式,直接采用弹性力学手段对其进行连续化分析较为困难,需将其等代为其他连续体——考虑结构剪切变形的拟夹层板。“拟夹层板法”(后简称拟板法)来源于对夹层板结构的受力性能研究[43],经董石麟等运用到平面网架结构[44, 45]和组合网架结构[46]的计算分析当中之后,再由马克俭、张华刚等改进后运用到空腹网架结构以及空腹夹层板结构的连续化分析当中[1, 22, 26],是经典的结构分析方法,也是现代计算力学的理论基础。
经过数年的理论研究工作,目前针对钢筋混凝土空腹夹层板结构,主要有两种拟板法计算模型:一种是完全基于弹性力学平衡方程的求解方法,将空腹夹层板分为上下表层和夹心层共三层(图2-1左)。其核心点在于对上下表层的薄膜刚度等代计算,以及对夹心层的平面外等代剪切刚度进行计算。最后将等代刚度列入平衡方程,得到空腹夹层板的挠度方程,当考虑夹层板的剪切变形时,方程表示为十阶的偏微分方程式;另一种拟板法的控制方程基于变分法建立,将应力作为自变量建立能量函数,利用拉格朗日乘子将应力结果作为约束条件,最后以求解方程参数类似的形式获得空腹夹层板的挠度方程。此种方法将空腹夹层板分为四层(图2-1右),从而将空腹夹层板分成了一块表面薄板、二块正交的网架和中间的剪力键夹心层。在计算结构受横向剪切影响时,将除表面薄板以外的构件同时考虑,在计算其他应力影响时,又当作不同厚度的拟板结构进行,从而增加计算精度。此方法同样需要计算其夹心层受平面外剪切的影响。由此可见,想要使用拟板法分析钢筋混凝土空腹夹层板,其夹心层的平面外等代剪切强度计算是十分重要的。
..............................
2.2 夹心层的平面外等代剪切刚度计算方法
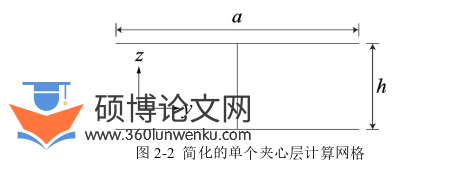
肖建春、张华刚等推导了夹心层的平面外等代剪切刚度计算方法[22, 25]。其核心在于将空腹夹层板夹心层的单个网格化简为平面的工字形结构,如图2-2所示,再使用虚功原理得到2.2 夹心层的平面外等代剪切刚度计算方法 肖建春、张华刚等推导了夹心层的平面外等代剪切刚度计算方法[22, 25]。其核心在于将空腹夹层板夹心层的单个网格化简为平面的工字形结构,如图2-2所示,再使用虚功原理得到
土木工程论文怎么写
目前空腹夹层板夹心层的平面外等代剪切刚度计算式未考虑结构的空间构型及泊松比等参数的影响,且计算出的等代剪切刚度的精确性难以保证。通过拟板法计算要得到精确的空腹夹层板的受力性能,就需要更精确的夹心层平面外抗剪强度参数。目前国内外研究者对类似夹芯板结构的平面外抗剪参数计算有不少研究方法:Du等采用能量法计算了甲虫翅鞘网格板平面内和平面外的等效剪切模量[47];Shi等应用数值方法改进了蜂窝板芯的平面外剪切刚度和局部剪切应力的表达式[48];Novak 等采用各项同性假设计算出了开孔泡沫的剪切模量[49];Praveen等通过动力学方法得到了复合材料下蜂窝芯的平面外剪切模量[50]。总结以上研究,可以看出国内外多将计算目标选择为更加精确的等效剪切模量。考虑到连续化分析的发展趋势以及计算难度,选择采用能量方法对夹心层的平面外等效剪切模量进行推导。
...............................
第三章 考虑节点刚域效应的梁-板单元模型分析方法研究 ............... 26
3.1 梁单元的节点误差分析............................ 26
3.2 钢筋混凝土空腹夹层板的梁单元计算模型假设 ........................ 27
第四章 基于超单元法的精细有限元模型分析方法研究 .................... 47
4.1 精细化有限元分析方法简介 ....................... 47
4.2 基于超单元法的钢筋混凝土空腹夹层板精细化有限元分析 .... 47
第五章 精细有限元法与梁-板模型分析方法对比研究 ....................... 63
5.1 有限元方法的选型 ........................... 63
5.2 两种方法计算对比分析.................... 63
第五章 精细有限元法与梁-板模型分析方法对比研究
5.1 有限元方法的选型
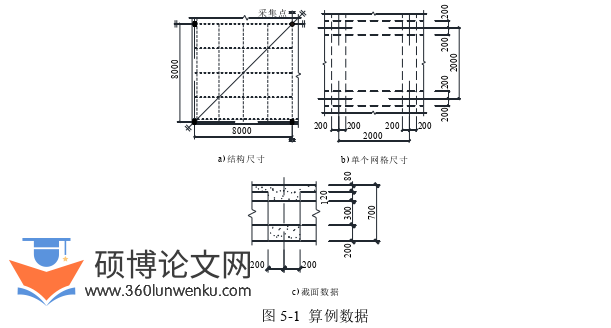
通过对钢筋混凝土空腹夹层板的有限元分析方法进行研究,共3种改良后的计算模型:基于高精度等效剪切模量的连续化偏微分方程有限元数值求解方法,基于梁-板单元模型的FeaR1和基于精细有限元的超C模型。有限元数值求解方法和FeaR1提高了梁单元的计算精度,超C模型提高了精细有限元的计算效率。由于偏微分方程有限元数值求解方法仅能考虑特殊工况下的情况,仅对比后两种有限元计算模型。为研究出适用于工程实际的空腹夹层板有限元模型,采用模型的算例计算结果对比的方式进行分析,以精细有限元的计算结果为基准,从计算精度、计算效率及使用难度等维度对该2种模型进行评价。
土木工程论文参考
..............................
第六章 结论与展望
6.1 研究结论
当前钢筋混凝土空腹夹层板的有限元计算方法过于陈旧,不能平衡其计算精度与计算效率。本文以钢筋混凝土空腹夹层板为研究对象,针对该结构的连续化分析方法和有限元分析方法进行研究。本文通过理论推导、案例分析以及有限元计算结果对比分析,对研究对象的连续化分析方法和有限元建模方法等方面进行了研究,提出两种钢筋混凝土空腹夹层板新型建模计算方法,得到主要结论如下:
对基于高精度等效剪切模量的连续化分析方法进行研究,发现该方法的计算核心点,即夹心层抗剪刚度的等代计算。以往方法中忽视对夹心层空间受力特性的考虑,且缺乏对建筑材料特性的表达。本文由此提出考虑空间构型的夹心层平面外等效剪切模量计算式,该计算式考虑了空腹夹层板的空间受力形式,并将材料剪切模量和泊松比纳入计算。通过对计算式的适用范围进行讨论,修正了计算式中的部分参数。通过等效方法计算出的切应变与精细有限元计算结果进行对比,其计算结果相比跟以往计算式精度有显著提高。通过其得到的空腹夹层板的连续化偏微分方程,在周边简支工况下计算精度提高5%。
对考虑节点刚域效应的梁-板单元模型分析方法进行研究,发现模型中梁单元作为梁柱结构,计算其交汇节点处会产生计算误差。本文对梁单元的计算方法进行研究,并提出假设:即在空腹夹层板的梁-板单元模型中存在节点刚域效应。为验证假设效应,取已有实验数据对比梁-板模型的有限元分析结果。在验证假设存在后,提出完全考虑节点刚域效应的梁单元FeaR1计算模型。将FeaR1与精细有限元模型进行计算精度对比分析,相较传统梁单元计算模型,FeaR1计算模型能恢复空腹夹层板平均95%的计算刚度遗失。在静动力分析中,FeaR1计算误差显著低于常规梁单元计算模型,适用于工程实际。
参考文献(略)
