本文是一篇土木工程论文,本篇论文对张拉整体结构形态生成理论进行了相对系统的研究与总结,尤其针对仅给定拓扑几何的张拉整体结构,在原有研究的基础上,从平衡矩阵变秩重构的角度,通过多种形式平衡矩阵组合应用,实现了张拉整体结构的形态生成。
第1章 绪论
1.1 引言
早期的张拉整体源于艺术领域的雕塑(见图1-1),这些雕塑展示了张拉整体结构的可调节性和自平衡特性。R.B.Fuller[1-4]为"张拉结构"的引入和推动做出了重要贡献,他将其视为自然界的基本原理,强调在保持稳定性的同时,也实现了轻量化和灵活性。R.B.Fuller强调设计的整体性和可持续性,并主张以资源的最优利用为目标的高效设计。正如他设计的“测地线穹顶”,是一种由杆和连接节点组成的结构,形成了一种类似于球体的形状,这种结构(见图1-2)不仅体现了张拉结构的原理,还具有卓越的强度和稳定性。“测地线穹顶”成为建筑界的标志性设计,对后世建筑师和设计师产生了深远影响。

土木工程论文怎么写
张拉整体(Tensegrity)一词结合了“张力”(tension)和“完整性”(integrity)这两个词。这种结构通过张拉元素(绳索或缆索)和压缩元素(柱或杆)的相互作用来保持平衡和稳定,形成了一种非常独特而复杂的结构。R.B.Fuller提出了工程和数学方面的知识,而Snelson[5]则通过他的雕塑实践为这一理念注入了艺术和形式美感。
在20世纪末,关于张拉整体结构理论方面的系统研究开始取得进展,涵盖了张拉整体结构的多个方面,在这一时期,代表学者包括:Motro[8-9],Pellegrino[29-31]等,深入研究了其力学性质和空间拓扑关系,推动了形态发现及实际应用的探索。他们的工作为张拉整体结构的理论和实际应用奠定了重要基础。
....................
1.2 张拉整体的定义及特点
1.2.1 定义
张拉整体结构是一种特殊的索杆张拉体系,它通过预应力技术实现自应力状态,以此提高结构的性能和稳定性。这种设计方法源于早期研究者(如Fuller、Snelson[4-5])的贡献,并由以下几个关键特征定义:
空间体系与自应力状态:张拉整体结构是一个预先通过拉伸力预应力化的空间体系,这种预应力化的过程使得结构元素在施工前就达到一种自应力状态,从而优化了性能;
受拉构件的连续性:受拉构件在结构中形成一个连续网络,且不具备抗压刚度,这表明它们在结构中担任着持续支撑的角色,而不是承受压缩力。
受压构件的间断布置:结构中的受压构件被间断地布置在不同的节点上,每个节点仅连接一根压杆,这种布局反映了受压构件的离散本质和节点连接的独特性质。
后续研究者则从几何学的角度进一步阐述了张拉整体,将其视为一个空间网格,其中的绳索和杆件代表节点之间的几何约束,进一步清晰地刻画了结构的几何属性。Motro提供了一个更为正式的定义,认为张拉整体结构是由一组连续的受拉单元和离散的受压单元组成的,这些元素相互作用形成了一个稳定的自平衡系统。
综上,张拉整体可以被定义为:一种采用预应力技术以实现自应力状态的空间结构体系,其由间断的受压构件和连续受拉构件通过精确的几何布局相互作用,共同形成了一个稳定且性能优越的整体。
........................................
第2章 结构形态生成分析基础
2.2 平衡矩阵理论与力密度法
2.2.1 平衡矩阵理论
索杆体系的主要构成元素:节点、杆单元、索单元。杆单元是指两端铰接并且具有一定抗弯刚度的二节点直线单元。索、杆单元的形态分析过程基本一致,都具有如下基本力学特性:两端节点铰接;索、杆单元主要承受轴向力,张拉整体结构由于其压杆通常是不连续的,主要承受压力,拉索则主要承受拉力,由这两者的相互作用,从而形成一个平衡的稳定体系。
经典矩阵力法列式中以应力或内力为基本未知量,通过平衡矩阵与外部载荷联系起来。对于由索杆单元构成的空间铰接体系,设体系j个节点,b个单元,对于某个节点i(见图2-1)
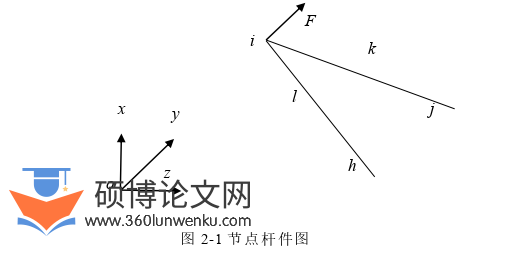
土木工程论文怎么写
.........................
2.5 本章小结
本章探讨了索杆张拉结构形态生成问题中,寻求内力分布与确定结构形状几何的经典方法——平衡矩阵理论与力密度法。基于关联矩阵显式的精确推导,揭示了这两种方法的基本理论框架:它们的核心都在于构建平衡方程,将形态生成的问题转化为矩阵求解的问题。总结比较了这两种方法所依据的平衡矩阵的两种不同表现形式,考虑到形态生成过程中基本未知量的差异,扩展了平衡矩阵的理论基础,推导出了平衡矩阵的六种形式。这六种形式的平衡方程,对应于六种不同的平衡矩阵以及各自的未知量,尽管表现形式各异,但本质上都是相互等价的平衡方程,它们之间可以通过数学变换实现互相转换。最后,对六种形式的平衡矩阵的零空间与列空间进行了深入讨论,揭示了它们在力学上、形态上的深刻意义,不仅阐明了在体系形态生成问题中,不同平衡矩阵形式之间的内在联系,也为理解和应用这些平衡矩阵提供了坚实的理论基础
...................................
第3章 拓扑找力分析 ............................ 30
3.1 引言 ............................ 30
3.2拓扑找力分析的基础理论 ............................ 30
第4章 自适应力密度法与平衡矩阵的变秩重构 ........................ 42
4.1 引言 ................................. 42
4.2 自适应力密度法 ........................................ 42
第5章 形态生成的一般算法 ................................ 58
5.1 引言 ........................................ 58
5.2形态生成与全域数值重构 .................... 58
第5章 形态生成的一般算法
5.2形态生成与全域数值重构
拓扑几何给定条件下,利用力密度平衡矩阵求解张拉整体结构的形态生成问题的关键在于:关联矩阵一定,通过更新力密度基本未知量,实现力密度平衡矩阵D的变秩重构。除了对角关联矩阵TC之外,其它形式平衡矩阵的重构都是对分块对角矩阵的重构,形态生成的一般算法是多种平衡矩阵的组合应用,其核心在于通过平衡矩阵基本未知量的更新,完成平衡矩阵的变秩重构,保证体系形状几何一定能够生成,同时对预应力体系一般还应保证独立自应力模态存在。
对角元基本未知量元素的数量远比平衡矩阵全部元素的数量少;各种形式的平衡矩阵乘积分解的第一项均为对角分块关联矩阵TC;平衡矩阵A、E、D、Ψ重构时可引入已知的构件方向矢量、已知的构件结点坐标之差、已知的构件力密度、已知的构件内力。可以采用全域数值重构引入各形式平衡矩阵的基本未知量。
土木工程论文参考
...........................
第6章 结论与展望
6.1结论
本文针对给定拓扑几何的张拉整体形态生成问题,通过各种形式的平衡矩阵对张拉整体结构的形态生成理论进行研究,主要结论如下:
(1)基于图论中关联矩阵来显式组装平衡矩阵的方法,在平衡矩阵理论与力密度法的启发下,推导出平衡矩阵的六种形式,并推导给出各形式平衡矩阵的零空间与列空间力学意义,对各形式平衡矩阵在形态生成过程中的应用做出了系统性的归纳。
(2)基于对各形式平衡矩阵的子空间研究,依据关联矩阵形式的平衡矩阵,提出了拓扑找力分析的概念,对于仅给定拓扑信息的张拉整体结构形态分析,更简洁和高效,可以不依赖于具体的形态,对张拉整体结构进行拓扑找力分析,检验给定的拓扑几何结构形态生成的可能性,能够节省计算时间。
(3)基于对自适应力密度法的理论研究与算法实现,提出平衡矩阵变秩重构的概念,力密度平衡矩阵的降秩是特定的拓扑几何与变化的力密度共同作用的结果,进一步从数学的角度推导出力密度平衡矩阵的变秩重构规律,并推广到其他形式的平衡矩阵。
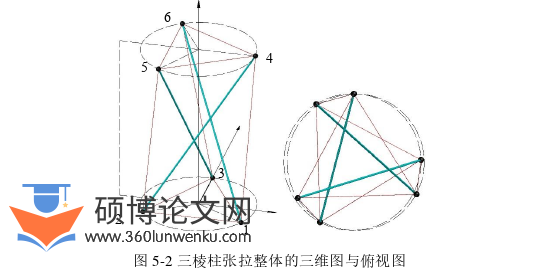
(4)基于各形式平衡矩阵在形态生成过程中的应用与平衡矩阵变秩重构的规律,尝试多种形式平衡矩阵的组合应用来求解拓扑给定的张拉整体形态生成问题。提出修正的自适应力密度法,作为解决这种类型问题的一般算法,以三棱柱张拉整体与星形张拉整体结构为案例,展示一般算法广泛的适用性。
综上所述,本篇论文对张拉整体结构形态生成理论进行了相对系统的研究与总结,尤其针对仅给定拓扑几何的张拉整体结构,在原有研究的基础上,从平衡矩阵变秩重构的角度,通过多种形式平衡矩阵组合应用,实现了张拉整体结构的形态生成。
参考文献(略)
