本文是一篇土木工程论文,本研究基于OpenSees有限元分析软件,对典型的四层、六层和八层延性钢筋混凝土框架在不同地震作用下进行有限元分析,为考虑地震动的不确定性,选择了共计150条地震动记录并进行调幅,以获得22037条地震响应数据,进而构建地震响应数据集。
第1章 绪论
1.1 研究背景与意义
我国是世界上地震活动最频繁的国家之一。地震不仅威胁着人们的生命和财产安全,还会引发社会不稳定等消极影响。地震频发地区受到的灾害影响尤为严重,对当地的生活和生产造成了极大破坏[1]。在我国,钢筋混凝土(RC)框架结构是数量最多、分布最广泛的建筑结构形式,同时,在建筑结构的实际工程应用中,钢筋混凝土也是最普遍采用的建筑材料之一。近些年来,由于地震灾害的发生越来越频繁[1-3],其对RC框架结构造成了严重的破坏。然而,尽管全世界发生了无数次地震灾害,但要准确获取地震作用下房屋建筑的倒塌响应数据却非常困难。由此,了解和预测多层钢筋混凝土结构的地震响应已成为迫切需要解决的问题。此外,随着基于性能抗震设计思想的发展[4],结构地震响应分析与预测也成为结构和地震工程领域研究的一个重要课题。
增量动力分析(IDA) [5]是一种考虑地震输入不确定性,对地震荷载作用下结构性能进行综合评估的地震工程计算分析方法[6-7]。其作为一种建立在非线性时程分析基础上的动力分析方法,能够考虑地震动(GM)输入的不确定性,因而可以合理、准确地量化结构的抗震性能。它捕获了结构系统在不同水平地震动下的响应,从线弹性行为到塑性行为再到完全倒塌。因此,这将为研究者探究随着地震烈度的变化结构的抗震性能如何变化提供一个更广阔的视野。为了生成IDA曲线,最经典的方法之一是对特定结构进行非线性动力时程分析,首先建立该结构的有限元模型,然后选择数十条地震动记录,每条GM记录必须进行多次缩放。最后,对分析模型在数百条GM记录下进行非线性时程分析,进而得到感兴趣的工程需求参数(EDPs)。得到的EDPs和相应的地震烈度等级被绘制成IDA曲线。当通过经典的传统方法来完成IDA曲线的生成时,IDA 计算过程需要大量的非线性时程动力分析结果[8],这极大地增加了计算成本,导致计算效率不高[9-10]。为了加速地震响应结果的生成,许多研究人员将注意力转向开发更简化的分析模型,以取代用于非线性结构动力分析的高保真有限元模型,其途经就是不断发展和完善时程分析法,比如发展和完善GM输入确定方法、结构及构件模型化方法、积分方法等;同时,为了减少计算量,用非线性静力分析代替非线性动力分析也进行了一些研究。
......................
1.2 国内外地震响应计算模型研究
1.2.1 传统的地震响应计算方法概述
随着研究者对结构体系在地震作用下性能发展的深入研究,地震动记录数据逐渐得到充实,新的地震响应计算方法被不断提出,因此,使得结构抗震理论的研究不断深入,从传统的结构地震响应计算方法的发展历程来看,其大致可以被分为三个主要阶段:静力阶段、反应谱阶段和动力时程分析阶段[14]。
1.2.1.2 反应谱方法
反应谱理论源于振型分解和反应谱的概念。它将单质点体系在地震激励下的最大反应值作为纵坐标,将单质点体系的自振周期(或自振频率)作为横坐标建立坐标系,然后将两者之间的对应关系绘制成曲线,形成反应谱。振型分解给出假定,将多自由度体系的地震响应看作是分解后的多个单自由度体系响应的叠加。反应谱理论包含如下三个基本假定[16-17]:
(1)假定结构体系的地震反应是线弹性的,该假定是振型组合叠加的前提;
(2)假定结构设计采用的反应谱是标准反应谱;
(3)假定结构体系最不利的地震响应与达到最大值附近的次数或概率无关,只与地震响应的最大绝对值相关。
...........................
第2章 基于LRLS-SVMR的RC框架IDA曲线预测模型性能研究
2.1 LRLS-SVMR 的数学模型构建
支持向量机是一种常用的机器学习算法,根据所用损失函数的类别,其数学模型构建过程可分为两种形式。一种是基于1范数的损失函数,称之为SVMR[57],其数学模型最终可归为求解一个二次规划问题。另一种是基于2范数的损失函数,称之为LS-SVMR[58],其数学模型最终可归为求解一个线性方程组。相较于求解二次规划问题,求解线性方程组更为简单和直接。因此,LS-SVMR能够极大地提高SVMR的训练过程,且能保持与其具有相当的非线性拟合能力[22]。
为了验证LRLS-SVMR方法计算RC框架工程需求参数的准确性和高效性,本研究以延性钢筋混凝土(RC)框架为例,分别设计了4层、6层以及8层3种延性RC框架结构,选择了共计150条地震动记录并进行调幅,用于考虑地震输入的不确定性[21],通过增量动力方法最终形成了22037个大规模样本数据,用于本章节数值案例分析。具体信息如下所述。
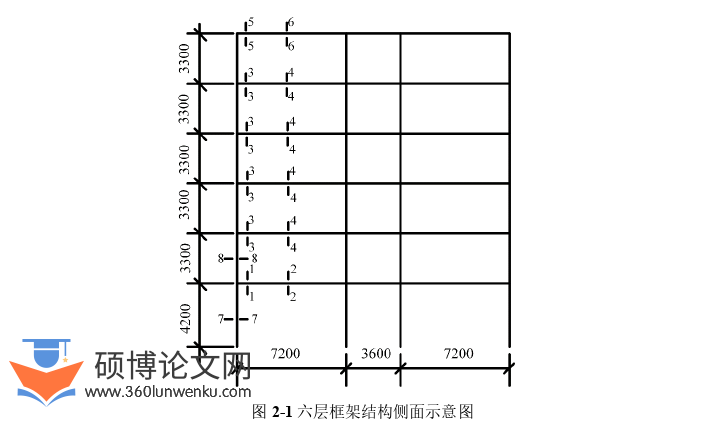
根据《建筑抗震设计规范(2016年版)》GB50011-2010[60]等规范要求,本文分别设计了4层、6层以及8层3种延性RC框架结构,其一阶自振周期分别为0.82s,1.07s,1.12s。以6层框架为例,结构的平面图,中间一榀框架、梁柱截面尺寸以及配筋图如图2-1,图2-2,图2-3所示,值得说明的是,本算例所有设计的RC框架梁截面均考虑了混凝土板的贡献,将矩形梁截面等效为T形截面,梁的T形截面翼缘考虑了板的贡献。其他框架的截面尺寸与配筋信息详见表2-1。三种结构的首层层高均为4.2m,其余层高均为3.3m,混凝土强度等级为C30,钢筋采用HRB400,框架楼层恒荷载标准值1.5kN/m2 ,活荷载标准值2.0kN/m2。场地类别为第Ⅱ类,场地特征周期Tg=0.40s,设计基本风压0.30kN/m2,地面粗糙类别为C类,抗震设防类别丙类,框架抗震等级为二级,抗震设防烈度为8度,设计基本地震加速度0.20g,地震分组为第二组,体现了我国地震易发区建筑工程的设防要求。
土木工程论文怎么写
.....................
2.3 LRLS-SVMR预测IDA曲线性能分析
2.3.1 与 LS-SVMR 模型对比:最大层间位移角预测
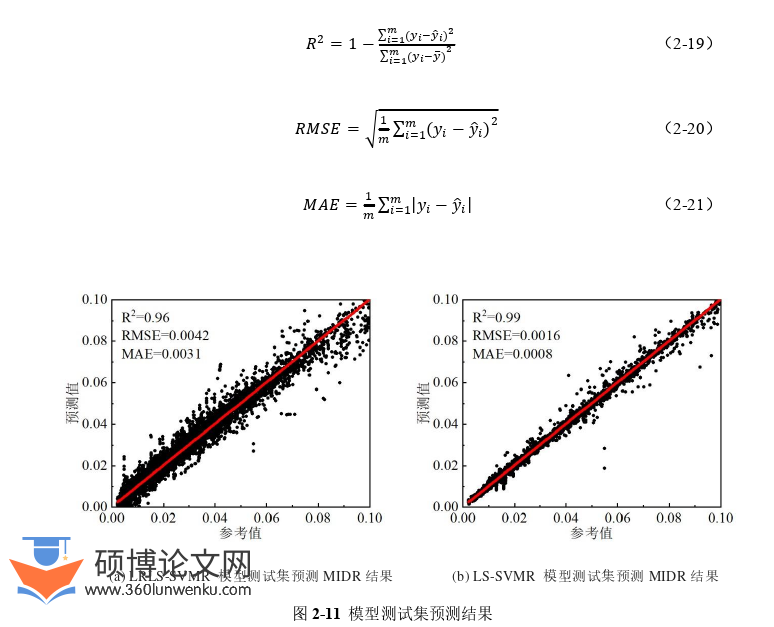
本节将上节构建的大规模样本数据{(????????,????????)}????=122037按照7:3的比例随机划分成训练集和测试集,最终训练集有15426个样本数据,测试集则为剩余的6611个样本数据。模型的预测性能采用决定系数(R2),均方根误差(RMSE)和平均绝对误差(MAE)来量化,其计算公式见式(2-19),(2-20),(2-21)。本文研究内容的所有代码均在Python中实现,所使用的计算机配置为Intel i9-10900K CPU,64GB内存。图2-11(a)为本文提出的LRLS-SVMR方法在测试集上的预测结果,其中R2达到0.96,RMSE达到0.0042,MAE达到0.0031。图2-11(b)为LS-SVMR方法在测试集数据上的预测结果,其中R2达到0.99,RMSE达到0.0016,MAE达到0.0008。需要说明的是,图2-11(a)为LRLS-SVMR基于从15426个训练数据中随机选择1000个数据构成低秩核矩阵的近似结果,而图2-11(b)则为LS-SVMR基于整个训练集(15426个数据)得到的结果。从结果对比可知,LRLS-SVMR模型仅利用1000个数据得到的结果与LS-SVMR利用15426个数据得到的结果相当,预测性能接近。
土木工程论文参考
..................................
第3章 基于递归采样理论的LRLS-SVMR模型性能研究 .......................... 30
3.1 递归采样嵌入LRLS-SVMR的数学模型构建 .................................. 30
3.1.1 自适应递归采样理论的数学模型 ............................................. 30
3.1.2 基于自适应递归采样的特征学习(RSFL)模型构建 ................. 32
第4章 RC框架设计变量-地震动参数与工程需求参数相关性分析 ........... 50
4.1 相关性分析概述 .................................. 50
4.2 RC框架设计变量与工程需求参数相关性分析 ................................. 51
第5章 结论与展望 ...................................... 59
5.1 结论 ........................................ 59
5.2 展望 .................................... 60
第4章 RC框架设计变量-地震动参数与工程需求参数相关性分析
4.1 相关性分析概述
相关分析是指对两个或多个具备相关性的变量元素进行分析[82],从而衡量两个因素的的相关密切程度,相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。而相关系数是反映两个变量之间线性相关程度的指标。相关系数最早是由统计学家卡尔·皮尔逊设计的统计指标[83-84],是研究变量之间线性相关程度的量,一般用字母 r 表示。由于研究对象的不同,相关系数有多种定义方式,较为常用的是皮尔逊相关系数( Pearson correlation coefficient),又称皮尔逊积矩相关系数(Pearson product-moment correlation coefficient,简称 PPMCC或PCCs),是用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。当接近1时,表示两者具有强烈的正相关性;当接近-1时,表示有强烈的的负相关性;而值接近0,则表示相关性很低。
皮尔逊相关系数的使用前提包括以下几点:(1)变量是连续变量:皮尔逊相关系数适用于两个连续性变量之间的关系。(2)线性关系:皮尔逊相关系数假设变量之间的关系是线性的,如果变量之间存在非线性关系,皮尔逊相关系数可能无法准确反映两个变量之间的关系。(3)变量是正态分布的:皮尔逊相关系数的计算基于变量的正态分布假设。(4)无异常值:皮尔逊相关系数对异常值比较敏感,异常值可能对相关系数的计算结果产生较大影响。
土木工程论文参考
............................
第5章 结论与展望
5.1 结论
本研究基于OpenSees有限元分析软件,对典型的四层、六层和八层延性钢筋混凝土框架在不同地震作用下进行有限元分析,为考虑地震动的不确定性,选择了共计150条地震动记录并进行调幅,以获得22037条地震响应数据,进而构建地震响应数据集。地震响应数据集的输入变量包括钢筋混凝土框架设计参数和地震动参数,输出变量为最大层间位移角。基于构建的地震响应数据集,开发了低秩矩阵引导支持向量机(LRLS-SVMR)的机器学习模型,在此基础上,对该模型选择子样本的策略进行优化,开发了基于自适应递归采样的特征学习(RSFL)机器学习模型,并分别开展了数值试验验证所提出模型的高效性和准确性。最后,分析了钢筋混凝土框架设计变量-地震动参数与工程需求参数的相关性,进而开发了图形用户界面,方便工程人员安全、准确、快速获得最大层间位移角和IDA曲线。本文的主要结论如下:
(1)在大规模训练数据下,LRLS-SVMR 能利用 Nystrom 近似理论建立一个小规模低秩核矩阵,用于近似大规模原核矩阵。这使得其训练过程能极大地提高计算效率且保持较高的预测性能。为了验证该方法的准确性和高效性,基于22037条地震响应数据,分别与支持向量机(LS-SVMR)和传统有限元方法进行对比。结果表明本研究提出的 LRLS-SVMR模型的预测性能和计算效率与子样本的规模有关,预测性能会随着子样本规模的增加而提高,但计算效率则会降低。通过与最小二乘支持向量机(LS-SVMR)模型对比,发现LRLS-SVMR 模型的预测性能与基于大规模训练样本得到的 LS-SVMR 模型性能相当,但 LRLS-SVMR 模型的计算时间却比 LS-SVMR 快了近140倍,显著地提高了计算效率。LRLS-SVMR 能准确预测 RC 框架的最大层间位移角和 IDA 曲线,其计算效率比 LS-SVMR 快了近140倍,其计算效率远远高于传统有限元计算方法。
参考文献(略)
