第 1 章 绪论
1.1 研究背景与意义
全球导航卫星系统(GNSS)以其定位快、精度高等优势在测绘、水利、交通、资源调查等领域广泛应用。但在高程方面,GNSS 提供的是大地高,不是法定的正常高。目前,水准测量和三角高程测量仍然是获得正常高的基本方法。而当下传统的水准测量和三角高程测量与 GNSS 测量相比,显得程序复杂,工作效率低下,在地形复杂和范围较大的测区也比较困难。因此,将 GNSS 高程测量与水准测量相结合的GNSS 水准测量应运而生,此方面的研究也在如火如荼地开展。
本文选择基于 EGM2008 模型与多面函数进行大地水准面拟合方法进行研究,充分利用了 EGM2008 模型的高精度和多面函数的便捷性特征,意在为创建实用的大地水准面精化实用方法与流程奠定基础。本文的研究成果对生产、教学和科研工作均具有参考意义。
1.1 研究背景与意义
全球导航卫星系统(GNSS)以其定位快、精度高等优势在测绘、水利、交通、资源调查等领域广泛应用。但在高程方面,GNSS 提供的是大地高,不是法定的正常高。目前,水准测量和三角高程测量仍然是获得正常高的基本方法。而当下传统的水准测量和三角高程测量与 GNSS 测量相比,显得程序复杂,工作效率低下,在地形复杂和范围较大的测区也比较困难。因此,将 GNSS 高程测量与水准测量相结合的GNSS 水准测量应运而生,此方面的研究也在如火如荼地开展。
本文选择基于 EGM2008 模型与多面函数进行大地水准面拟合方法进行研究,充分利用了 EGM2008 模型的高精度和多面函数的便捷性特征,意在为创建实用的大地水准面精化实用方法与流程奠定基础。本文的研究成果对生产、教学和科研工作均具有参考意义。
.........................
1.2 国内外研究现状根据本文的研究内容,以下将从 EGM2008 地球重力场模型、多面函数拟合、多项式拟合三个方面的问题,就查阅到的文献资料进行分析、综述。
1.2.1 EGM2008 模型
当测量工作区高程起伏不大、地势相对平坦,面积不大时,采用二次曲面拟合法、三次曲面拟合法以及顾及 EGM2008 模型的似大地水准面精化方法,均能达到三等水准测量等级精度要求,能够用于实际测量,提高工作效率[1]。
依据高精度的、大范围的地面重力数据,建立的新一代全球重力场模型EGM2008。它的阶次已扩展到了 2190(带一些附加项后由 2159 阶次扩展而成),是一个完全阶次为 2190 的全球重力场模型,全球覆盖率为 83.3%[2]。
EGM2008 模型可以达到很高的精度,在我国大陆地区进行的测试结果表明,EGM2008 模型在我国大陆地区的总体精度与 EGM2008 模型在全球范围内的精度相当。与 WDM 94、DQM 系列、EGM96 相比,EGM2008 模型求出的高程异常精度提高了 3-5 倍,比利用 GRACE 数据的 IGG05b、EIGEN-5c 模型提高了 2 倍以上[3]。
由于 EGM2008 模型的现势性不好,有学者提出对于 EGM2008 模型进行了两项改椭球面不平行性改正和剩余地形改正。
1.2.1 EGM2008 模型
当测量工作区高程起伏不大、地势相对平坦,面积不大时,采用二次曲面拟合法、三次曲面拟合法以及顾及 EGM2008 模型的似大地水准面精化方法,均能达到三等水准测量等级精度要求,能够用于实际测量,提高工作效率[1]。
依据高精度的、大范围的地面重力数据,建立的新一代全球重力场模型EGM2008。它的阶次已扩展到了 2190(带一些附加项后由 2159 阶次扩展而成),是一个完全阶次为 2190 的全球重力场模型,全球覆盖率为 83.3%[2]。
EGM2008 模型可以达到很高的精度,在我国大陆地区进行的测试结果表明,EGM2008 模型在我国大陆地区的总体精度与 EGM2008 模型在全球范围内的精度相当。与 WDM 94、DQM 系列、EGM96 相比,EGM2008 模型求出的高程异常精度提高了 3-5 倍,比利用 GRACE 数据的 IGG05b、EIGEN-5c 模型提高了 2 倍以上[3]。
由于 EGM2008 模型的现势性不好,有学者提出对于 EGM2008 模型进行了两项改椭球面不平行性改正和剩余地形改正。
.......................
第 2 章 EGM2008 模型及其使用
2.1 地球重力场模型
地球重力场模型从本质上来说就是一系列描述地球重力场的基本参数的集合,是对于实际的地球重力场的一种近似表达。从一般意义上说,任何一类能以一定的精度和分辨率确定重力场的参数集合都是一种重力场模型,例如,具有一定密度分布的离散点重力值集合;格网平均重力异常集合;重力位球谐或椭球谐展开系数集合等。从应用上来说,现今习惯上称全球 (或局部) 扰动重力位球谐展开系数集合为全球 (或局部) 重力场模型。
地球重力位的数学表达就是地球重力场模型,比较常用的就是用球谐函数的级数来表示。一个逼近地球外部引力位,且在无穷远处收敛至零的调和函数就是地球重力场模型,通常展开成一个在理论上收敛的整阶次球谐或椭球谐函数的无穷级数,一个级数展开的系数的集合就可以定义一个相应的地球重力场模型。任何一种和地球重力场同种构造的多项式系数,都可以构成重力场模型,但是,通常被使用的地球重力场模型,主要是指球谐函数和椭球谐函数的结合,也称为地球位系数,或者简称位系数。根据所逼近对象的不同,地球位系数分为重力位系数和扰动位系数,前者描述的是地球重力场,后者描述的是地球扰动重力场。
2.1 地球重力场模型
地球重力场模型从本质上来说就是一系列描述地球重力场的基本参数的集合,是对于实际的地球重力场的一种近似表达。从一般意义上说,任何一类能以一定的精度和分辨率确定重力场的参数集合都是一种重力场模型,例如,具有一定密度分布的离散点重力值集合;格网平均重力异常集合;重力位球谐或椭球谐展开系数集合等。从应用上来说,现今习惯上称全球 (或局部) 扰动重力位球谐展开系数集合为全球 (或局部) 重力场模型。
地球重力位的数学表达就是地球重力场模型,比较常用的就是用球谐函数的级数来表示。一个逼近地球外部引力位,且在无穷远处收敛至零的调和函数就是地球重力场模型,通常展开成一个在理论上收敛的整阶次球谐或椭球谐函数的无穷级数,一个级数展开的系数的集合就可以定义一个相应的地球重力场模型。任何一种和地球重力场同种构造的多项式系数,都可以构成重力场模型,但是,通常被使用的地球重力场模型,主要是指球谐函数和椭球谐函数的结合,也称为地球位系数,或者简称位系数。根据所逼近对象的不同,地球位系数分为重力位系数和扰动位系数,前者描述的是地球重力场,后者描述的是地球扰动重力场。
地球重力场模型实质上是地球重力场基础数据——平均重力异常的解析形式,但它在理论研究和实际应用中具有独特的完美性和方便之处。理论上,平均重力异常是空域数据,而地球重力场模型是频域信息。因此,后者对于以下几个方面都具有其重要意义和巨大作用,研究地球重力场的数学物理结构、探究并揭示其频谱特性、寻找实际应用的理论依据、指导实际应用的不断深入发展。实际应用中,一般将复杂的地球重力场解析化,并基于扰动位的泛函,可以十分方便地表示和提供大地水准面、重力异常、垂线偏差、扰动重力等扰动位的派生物。这种理论和实际应用上的优势,使得地球重力场模型在大地测量学、地球物理学、地球动力学、地质学、海洋学、生物学、空间和军事等学科和领域具有十分广阔的应用前景。
..........................
..........................
2.2 EGM2008 模型
GRACE 重力卫星数据表达了卫星在地球重力场中受到的摄动情况;该卫星可以精确的测量海洋部分的重力场情况,与海洋部分相比,该卫星在地面部分对于重力场测量的精度要更高。TOPEX 卫星,于 1992 年 8 月 10 日发射,其目的是用于地图海洋表面地形,是海洋学的革命,也证明了卫星海洋观测的价值。目前EGM2008 全球重力场模型是使用最广泛的重力场模型,阶次完全至 2159。EGM2008 采用当时最新的地形数据 DTM2006.0,该模型是由 EGM2008 模型研究小组研发的全球地形模型。EGM2008 模型的坐标系是 WGS-84(G1674)坐标系,
GRACE 重力卫星数据表达了卫星在地球重力场中受到的摄动情况;该卫星可以精确的测量海洋部分的重力场情况,与海洋部分相比,该卫星在地面部分对于重力场测量的精度要更高。TOPEX 卫星,于 1992 年 8 月 10 日发射,其目的是用于地图海洋表面地形,是海洋学的革命,也证明了卫星海洋观测的价值。目前EGM2008 全球重力场模型是使用最广泛的重力场模型,阶次完全至 2159。EGM2008 采用当时最新的地形数据 DTM2006.0,该模型是由 EGM2008 模型研究小组研发的全球地形模型。EGM2008 模型的坐标系是 WGS-84(G1674)坐标系,
是基于 ITRF2008 框架、2005.0 历元的。
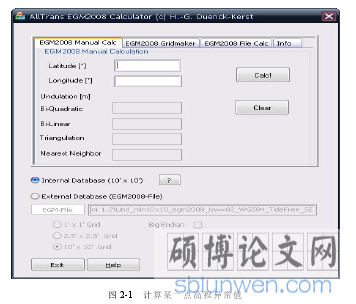
EGM2008 模型在中国大陆地区的精度约为20cm,其中在中国西部地区为 24cm,华北地区为 9cm,华东华中地区为 12cm。由于 EGM2008 模型的分辨率是有限制的,不能满足某些工程项目所需要的精度,想要得到的值往往需要需要使用数学内插的方式获取,在内插的过程中,信息的截断误差由此而产生,对于最后的结果产生了一定的偏差,而且 EGM2008 模型所使用的高程基准与测区的高程基准在很多情况下是不一致的,所以在进行 GNSS 高程拟合时,直接使用 EGM2008 模型进行计算得到的结果的精度在通常情况下是不能够保证的。
...........................
EGM2008 模型在中国大陆地区的精度约为20cm,其中在中国西部地区为 24cm,华北地区为 9cm,华东华中地区为 12cm。由于 EGM2008 模型的分辨率是有限制的,不能满足某些工程项目所需要的精度,想要得到的值往往需要需要使用数学内插的方式获取,在内插的过程中,信息的截断误差由此而产生,对于最后的结果产生了一定的偏差,而且 EGM2008 模型所使用的高程基准与测区的高程基准在很多情况下是不一致的,所以在进行 GNSS 高程拟合时,直接使用 EGM2008 模型进行计算得到的结果的精度在通常情况下是不能够保证的。

...........................
第 3 章 GNSS 水准拟合常用的方法............................27
3.1 多项式拟合法...................................27
3.1.1 多项式拟合拟合原理.................................27
3.1.2 降低多项式拟合中条件数的措施........................29
第 4 章 香港大地水准面精化实验与分析.........................35
4.1 香港的高程系统..............................................35
4.2 香港大地水准面控制点的测量....................................35
4.3 控制点观测高程异常与模型高程异常的比较分析.......................39
第 5 章 结论与展望......................................68
5.1 研究过程中遇到的问题及其处理....................................68
5.2 研究结论....................................69
5.3 不足与展望...............................69
第 4 章 香港大地水准面精化实验与分析
4.1 香港的高程系统
高程基准通常是根据平均海平面的某个关系确定的。香港现在用作高程控制的高程基准有两个,一是香港高程基准面(HKPD)以及海图深度基准面(CD)。
香港地图及图则上所有的高程,都是以香港高程基准面为基准的。这个基准以前称之为军用基准面(Oranance Datum)。
所有深度及海图上的等深线,均采用海图深度基准面 Chart Datum(CD)为起算面。这个基准面前称为海军基准面(Admiralty Datum)。
(1)香港高程基准面(HKPD)
在 1866 年,英国海军测量船(利福民号)用一粒铜制螺丝钉,在香港海军船厂内建立了一个水准点,杜伯克博士(Dr.Doberck)于 1887 年至 1888 年所确定的香港高程基准面,测定该水准点的高程为 5.435 米,此水准点的标志为利福民号的螺钉(Rifleman's Bolt),当时的香港高程基准位于平均海平面之下的 1.125 米。
香港天文台使用维多利亚港北角记录了 19 年(1965 至 1983 年)的验潮数据,重新确定了香港高程基准面为平均海平面之下约 1.23 米。利福民号的螺钉后来被移到了添马监海军基地普乐大厦的东面墙壁。并且在1984 年 5 月进行了重新测量,测得的高程位于 HKPD 之上 5.420 米。由于具有历史价值,当局将铜螺钉保留,但是不再作为高程基准的用途。
............................
4.1 香港的高程系统
高程基准通常是根据平均海平面的某个关系确定的。香港现在用作高程控制的高程基准有两个,一是香港高程基准面(HKPD)以及海图深度基准面(CD)。
香港地图及图则上所有的高程,都是以香港高程基准面为基准的。这个基准以前称之为军用基准面(Oranance Datum)。
所有深度及海图上的等深线,均采用海图深度基准面 Chart Datum(CD)为起算面。这个基准面前称为海军基准面(Admiralty Datum)。
(1)香港高程基准面(HKPD)
在 1866 年,英国海军测量船(利福民号)用一粒铜制螺丝钉,在香港海军船厂内建立了一个水准点,杜伯克博士(Dr.Doberck)于 1887 年至 1888 年所确定的香港高程基准面,测定该水准点的高程为 5.435 米,此水准点的标志为利福民号的螺钉(Rifleman's Bolt),当时的香港高程基准位于平均海平面之下的 1.125 米。
香港天文台使用维多利亚港北角记录了 19 年(1965 至 1983 年)的验潮数据,重新确定了香港高程基准面为平均海平面之下约 1.23 米。利福民号的螺钉后来被移到了添马监海军基地普乐大厦的东面墙壁。并且在1984 年 5 月进行了重新测量,测得的高程位于 HKPD 之上 5.420 米。由于具有历史价值,当局将铜螺钉保留,但是不再作为高程基准的用途。
............................
第 5 章 结论与展望
5.1 研究过程中遇到的问题及其处理
(1) SRTM 高程的提取
在提取 SRTM 高程时有多种办法,可以通过对 SRTM 数据进行降频处理,这里涉及到数字信号处理的知识,需要考虑时域、频域以及时频变换的问题,处理起来比较麻烦,所以没有使用此种方法;也可以使用物理大地测量中的球谐函数对 SRTM数据进行数据格式的转化,转化为系数格式的数据,进而求出所需要的 SRTM 高,但是此种方法的计算量很大,实施起来不是很容易。所以本文采用了使用 Arc Gis 进行 SRTM 高程的提取,此种方法比较直观易于理解,而且在操作上也比较简单。
5.1 研究过程中遇到的问题及其处理
(1) SRTM 高程的提取
在提取 SRTM 高程时有多种办法,可以通过对 SRTM 数据进行降频处理,这里涉及到数字信号处理的知识,需要考虑时域、频域以及时频变换的问题,处理起来比较麻烦,所以没有使用此种方法;也可以使用物理大地测量中的球谐函数对 SRTM数据进行数据格式的转化,转化为系数格式的数据,进而求出所需要的 SRTM 高,但是此种方法的计算量很大,实施起来不是很容易。所以本文采用了使用 Arc Gis 进行 SRTM 高程的提取,此种方法比较直观易于理解,而且在操作上也比较简单。
(2) 完全规格化的缔合勒让德函数求取
在计算完全规格化缔合勒让德函数时,有多种计算方法。①先计算缔合勒让德函数,然后在乘以完全规格化系数,就可以得到完全规格化的缔合勒让德函数。②采用垂直方向和对角线方向进行递推。③采用水平方向和对角线方向进行递推。④Belikov 算法。根据对于这几种算法的理解程度,选取其中一种作为在本文中计算完全规格化缔合勒让德函数的方法,在计算时,要灵活使用递归函数使计算变得更快捷,更利于理解,由于在计算时循环计算较多,所以本文在计算完全规格化缔合勒让德函数的时,使用了 Matlab 进行辅助计算,大大减少了计算量。
(3) DTM 高程的提取本文使用的 DTM 数据为 EGM2008 模型研发小组研制的 DTM2006.0 全球地形模型,DTM2006.0 的数据格式为系数形式的,大约 240 万对,在计算 DTM 高程时需要将每对系数都带入到公式中求值,在计算时使用 Matlab 辅助计算,在编程以采用读取文件的方式将 240 万对系数读取,加快了计算的速度,但是由于数据量较大,所以计算时间还是较长。
参考文献(略)
(3) DTM 高程的提取本文使用的 DTM 数据为 EGM2008 模型研发小组研制的 DTM2006.0 全球地形模型,DTM2006.0 的数据格式为系数形式的,大约 240 万对,在计算 DTM 高程时需要将每对系数都带入到公式中求值,在计算时使用 Matlab 辅助计算,在编程以采用读取文件的方式将 240 万对系数读取,加快了计算的速度,但是由于数据量较大,所以计算时间还是较长。
参考文献(略)
